题目内容
如图,已知圆 内接四边形
内接四边形 ,
,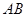 切圆
切圆 于点
于点 ,且与四边形
,且与四边形 对角线
对角线 延长线交于点
延长线交于点 ,
,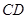 切圆O于点
切圆O于点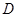 ,且与
,且与 延长线交于点
延长线交于点 ,延长
,延长 交
交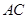 于点
于点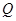 ,若
,若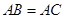 .
.
(1)求证: ;
;
(2)求证: 四点共圆.
四点共圆.
(1)详见解析;(2)详见解析.
解析试题分析:(1)两直线平行通常从三角形相似或角的关系考虑,条件可用的有两点一是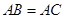 ,二是
,二是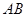 切圆
切圆 于点
于点 ,此条件可进一步挖掘出切割线定理,从而得到两个三角形相似,进一步得到两直线平行;(2)四点共圆经常从四边形对角互补考虑,借助于(1)的结论再向前跨近一步就离结论不远了.
,此条件可进一步挖掘出切割线定理,从而得到两个三角形相似,进一步得到两直线平行;(2)四点共圆经常从四边形对角互补考虑,借助于(1)的结论再向前跨近一步就离结论不远了.
试题解析:(1)若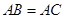 ,由切割线定理得
,由切割线定理得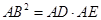 ,即
,即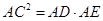 ,即
,即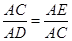 ,又
,又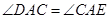 ,所以
,所以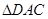 ∽
∽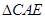
得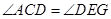 ,又
,又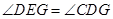
所以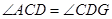 ,故
,故 .
.
(2)延长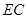 到
到 ,由
,由 ,得
,得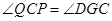 ,因为
,因为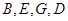 四点共圆,所以
四点共圆,所以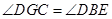
所以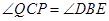 ,即
,即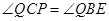
所以 四点共圆.
四点共圆.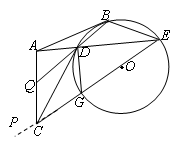
考点:直线与圆、圆与四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是圆
是圆 的切线,切点为
的切线,切点为 ,
,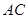 是圆
是圆 与圆
与圆 ,
,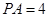 ,圆
,圆 ,那么
,那么 。
。
 是⊙
是⊙ 于点
于点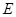 ,
, 平分
平分 .
. 是⊙
是⊙ ,求
,求
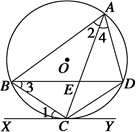
 是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE,
是的内接三角形,PA是圆O的切线,切点为A,PB交AC于点E,交圆O于点D,PA=PE, ,PD=1,DB=8.
,PD=1,DB=8.
 的面积;
的面积; ,且
,且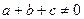 ,
,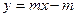 一定不通过第 象限.
一定不通过第 象限.
 的面积是1cm2,则
的面积是1cm2,则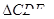 的面积是 cm2.
的面积是 cm2.