题目内容
四棱锥S-ABCD的底面ABCD是边长为2
的正方形,顶点在底面的投影是底面的中心,且该四棱锥的体积为12,则底面与侧面所成二面角的大小为
| 3 |
60°
60°
.分析:先计算四棱锥的底面ABCD的面积是12,再计算侧面积,利用公式即可得到结论.
解答:解:∵四棱锥S-ABCD的底面ABCD是边长为2
的正方形,顶点在底面的投影是底面的中心
∴四棱锥S-ABCD是正四棱锥,底面ABCD的面积是12
设正四棱锥的高为h
∵四棱锥的体积为12
∴
×12×h=12
∴h=3
∴正四棱锥的斜高为
=2
∴正四棱锥的侧面积为4×
×2
×2
=24
设底面与侧面所成二面角为α
∴cosα=
=
∴α=60°
故答案为:60°.
| 3 |
∴四棱锥S-ABCD是正四棱锥,底面ABCD的面积是12
设正四棱锥的高为h
∵四棱锥的体积为12
∴
| 1 |
| 3 |
∴h=3
∴正四棱锥的斜高为
32+(
|
| 3 |
∴正四棱锥的侧面积为4×
| 1 |
| 2 |
| 3 |
| 3 |
设底面与侧面所成二面角为α
∴cosα=
| 12 |
| 24 |
| 1 |
| 2 |
∴α=60°
故答案为:60°.
点评:本题解题的关键是确定四棱锥S-ABCD是正四棱锥,计算四棱锥的底面ABCD的面积、侧面积,属于基础题.

练习册系列答案
相关题目
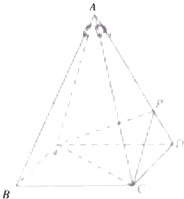 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的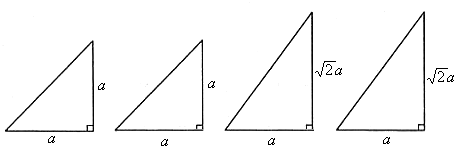
 (2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.
(2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示. 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=