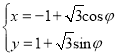题目内容
【题目】已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,圆
两点,圆![]() 是以线段
是以线段![]() 为直径的圆.
为直径的圆.
(1)证明:坐标原点![]() 在圆
在圆![]() 上;
上;
(2)设圆![]() 过点
过点![]() ,求直线
,求直线![]() 与圆
与圆![]() 的方程.
的方程.
【答案】(1)证明见解析;(2)当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .当
.当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
【解析】
(1)设![]() ,
,![]() ,
,![]() ,与抛物线方程联立可得
,与抛物线方程联立可得![]() ,
,![]() ,可证
,可证![]() 的斜率与
的斜率与![]() 的斜率之积为
的斜率之积为![]() ,即可得证明结论.
,即可得证明结论.
(2)因为圆![]() 的直径为
的直径为![]() ,且过点
,且过点![]() ,由圆的性质得出
,由圆的性质得出![]() ,结合(1)中的韦达定理,代数化简求得
,结合(1)中的韦达定理,代数化简求得![]() 的值,因此得出直线
的值,因此得出直线![]() 的方程和圆
的方程和圆![]() 的方程.
的方程.
解:(1)证明:设![]() ,
,![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,则
,则![]() .
.
又![]() ,
,![]() ,故
,故![]() .
.
因此![]() 的斜率与
的斜率与![]() 的斜率之积为
的斜率之积为![]() ,
,
所以![]() ,故坐标原点
,故坐标原点![]() 在圆
在圆![]() 上.
上.
(2)由(1)可得![]() ,
,
![]() ,
,
故圆心![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 的半径
的半径![]() .
.
由于圆![]() 过点
过点![]() ,因此
,因此![]() ,
,
故![]() ,
,
即![]() ,
,
由(1)可知![]() ,
,![]() ,
,
所以![]() ,解得
,解得![]() ,或
,或![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆心
,圆心![]() 的坐标为
的坐标为![]() ,
,
圆![]() 的半径为
的半径为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,圆心
,圆心![]() 的坐标为
的坐标为![]() ,
,
圆![]() 的半径为
的半径为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹记数法中,以“纵式”和“横式”两种方式来表示数字,如下表:
数字形式 |
|
|
|
|
|
|
|
|
|
纵式 |
|
|
|
|
|
|
|
|
|
横式 |
|
|
|
|
|
|
|
|
|
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图所示.如果把![]() 根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为______.
根算筹以适当的方式全部放入下面的表格中,那么可以表示的三位数的个数为______.
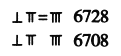
【题目】(本小题满分12分)某商场为了了解顾客的购物信息,随机的在商场收集了100位顾客购物的相关数据,整理如下:
一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) | [200,+∞) |
顾客人数 | m | 20 | 30 | n | 10 |
统计结果显示100位顾客中购物款不低于100元的顾客占60%,据统计该商场每日大约有5000名顾客,为了增加商场销售额度,对一次性购物不低于100元的顾客发放纪念品(每人一件).(注:视频率为概率)
(1)试确定![]() 的值,并估计该商场每日应准备纪念品的数量;
的值,并估计该商场每日应准备纪念品的数量;
(2)为了迎接店庆,商场进行让利活动,一次购物款200元及以上的一次返利30元;一次性购物
款小于200元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) | [0,50) | [50,100) | [100,150) | [150,200) |
返利百分比 | 0 | 6% | 8% | 10% |
估计该商场日均让利多少元?