题目内容
已知p:|1-| x-1 | 3 |
分析:思路一:“按题索骥”--解不等式,求否命题,再根据充要条件的集合表示进行求解;
思路二:本题也可以根据四种命题间的关系进行等价转换,然后再根据充要条件的集合表示进行求解.
思路二:本题也可以根据四种命题间的关系进行等价转换,然后再根据充要条件的集合表示进行求解.
解答:解:解法一:由p:|1-
|≤2,解得-2≤x≤10,
∴“非p”:A={x|x>10或x<-2}、(3分)
由q:x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴“非q”:B={x|x>1+m或x<1-m,m>0=(6分)
由“非p”是“非q”的必要而不充分条件可知:B⊆A.
解得m≥9.
∴满足条件的m的取值范围为{m|m≥9}.(12分)
解法二:由“非p”是“非q”的必要而不充分条件.即“非q”?“非p”,但“非p”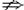 “非q”,可以等价转换为它的逆否命题:“p?q,但q
“非q”,可以等价转换为它的逆否命题:“p?q,但q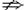 p”.即p是q的充分而不必要条件.
p”.即p是q的充分而不必要条件.
由|1-
|≤2,解得-2≤x≤10,
∴p={x|-2≤x≤10}
由x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴q={x|1-m≤x≤1+m,m>0}
由p是q的充分而不必要条件可知:
p⊆q?
解得m≥9.
∴满足条件的m的取值范围为{m|m≥9}.
| x-1 |
| 3 |
∴“非p”:A={x|x>10或x<-2}、(3分)
由q:x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴“非q”:B={x|x>1+m或x<1-m,m>0=(6分)
由“非p”是“非q”的必要而不充分条件可知:B⊆A.
|
∴满足条件的m的取值范围为{m|m≥9}.(12分)
解法二:由“非p”是“非q”的必要而不充分条件.即“非q”?“非p”,但“非p”
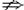 “非q”,可以等价转换为它的逆否命题:“p?q,但q
“非q”,可以等价转换为它的逆否命题:“p?q,但q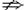 p”.即p是q的充分而不必要条件.
p”.即p是q的充分而不必要条件.由|1-
| x-1 |
| 3 |
∴p={x|-2≤x≤10}
由x2-2x+1-m2≤0,解得1-m≤x≤1+m(m>0)
∴q={x|1-m≤x≤1+m,m>0}
由p是q的充分而不必要条件可知:
p⊆q?
|
∴满足条件的m的取值范围为{m|m≥9}.
点评:本题考查了绝对值不等式与一元二次不等式的解法,又考了命题间的关系的理解;两个知识点的简单结合构成了一道难度不太大但是要么得分不高,要么因为这道题导致整张卷子答不完,所以对于此类问题要平时加强计算能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,x∈[
,x∈[ ,4].
,4]. );
); ,
,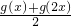 +
+ ,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围. ,x∈[
,x∈[ ,4].
,4]. );
); ,
, ],则f1(x)=-1,x∈[-
],则f1(x)=-1,x∈[- ,
, ],f2(x)=sinx,x∈[-
],f2(x)=sinx,x∈[- ,
, ],设φ(x)=
],设φ(x)= +
+ ,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.
,不等式p≤φ1(x)-φ2(x)≤m恒成立,求p、m的取值范围.