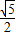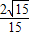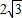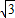题目内容
我们知道,在平面直角坐标系中,方程
+
=1表示的图形是一条直线,具有特定性质:“在x轴,y轴上的截距分别为a,b”;类比到空间直角坐标系中,方程
+
+z=1表示的点集对应的图形也具有某特定性质,设此图形为m,若m与zoy平面所成角正弦值为
,则正数λ的值是( )
| x |
| a |
| y |
| b |
| x |
| λ |
| y | ||
|
2
| ||
| 5 |
分析:由题意,方程
+
+z=1表示平面,且在x轴,y轴,z轴上的截距分别为λ,
,1,利用m与zoy平面所成角正弦值为
,结合等面积,即可求得结论.
| x |
| λ |
| y | ||
|
| 3 |
2
| ||
| 5 |
解答:解:由题意,方程
+
+z=1表示平面,且在x轴,y轴,z轴上的截距分别为λ,
,1
设平面与x轴,y轴,z轴的交点分别为A,B,C,△ABC中,BC边上的高为h,则
∵m与zoy平面所成角正弦值为
,
∴
=
,∴h=
λ
∵cosC=
=
∴sinC=
=
∵BC=2
∴由等面积可得
•2•
λ=
•2•
•
∴λ=
故选D.
| x |
| λ |
| y | ||
|
| 3 |
设平面与x轴,y轴,z轴的交点分别为A,B,C,△ABC中,BC边上的高为h,则
∵m与zoy平面所成角正弦值为
2
| ||
| 5 |
∴
2
| ||
| 5 |
| λ |
| h |
| ||
| 2 |
∵cosC=
| AC2+BC2-AB2 |
| 2AC•BC |
| 1 | ||
2
|
∴sinC=
| 1-cos2C |
| ||
2
|
∵BC=2
∴由等面积可得
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1+λ2 |
| ||
2
|
∴λ=
| 3 |
故选D.
点评:本题考查的知识点是类比推理,考查三角形面积的计算,属于基础题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
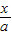 +
+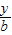 =1表示的图形是一条直线,具有特定性质:“在x轴,y轴上的截距分别为a,b”;类比到空间直角坐标系中,方程
=1表示的图形是一条直线,具有特定性质:“在x轴,y轴上的截距分别为a,b”;类比到空间直角坐标系中,方程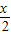 +
+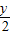 +z=1表示的点集对应的图形也具有某特定性质,设此图形为α,则坐标原点到α的距离是( )
+z=1表示的点集对应的图形也具有某特定性质,设此图形为α,则坐标原点到α的距离是( )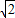
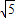
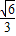
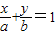 表示的图形是一条直线,具有特定性质:“在x轴,y轴上的截距分别为a,b”;类比到空间直角坐标系中,方程
表示的图形是一条直线,具有特定性质:“在x轴,y轴上的截距分别为a,b”;类比到空间直角坐标系中,方程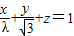 表示的点集对应的图形也具有某特定性质,设此图形为m,若m与zoy平面所成角正弦值为
表示的点集对应的图形也具有某特定性质,设此图形为m,若m与zoy平面所成角正弦值为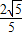 ,则正数λ的值是( )
,则正数λ的值是( )