题目内容
15.在△ABC中,∠ABC=60°,AB=2,BC=3,在BC上任取一点D,使△ABD为钝角三角形的概率为$\frac{1}{3}$.分析 满足条件的事件是组成钝角三角形,包括两种情况,第一种∠ADB为钝角,第二种∠BAD为钝角,根据几何概型的概率公式进行计算即可.
解答 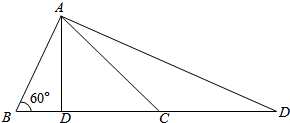 解:由题意知本题是一个等可能事件的概率,试验发生包含的事件对应的是长度为3的一条线段,
解:由题意知本题是一个等可能事件的概率,试验发生包含的事件对应的是长度为3的一条线段,
满足条件的事件是组成钝角三角形,包括两种情况
第一种∠ADB为钝角,这种情况的分界是∠ADB=90°的时候,此时BD=1
∴这种情况下,满足要求的0<BD<1.
第二种∠BAD为钝角,这种情况的分界是∠BAD=90°的时候,此时BD=4
∴这种情况下,不可能
综合两种情况,若△ABD为钝角三角形,则0<BD<1
P=$\frac{1}{3}$
故答案为:$\frac{1}{3}$
点评 本题考查了几何概率的求解,根据几何概型的概率公式是解决本题的关键.

练习册系列答案
相关题目
6.(文)已知复数z=6+8i,则-|z|=( )
| A. | -5 | B. | -10 | C. | $\frac{14}{9}$ | D. | -$\frac{16}{9}$ |
7.已知复数z=2-i,则$\frac{z+1}{\overline{z}-1}$的虚部为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
4.已知A(2t,t+2,2),B(1+t,2t-1,-2),则|AB|的最小值为( )
| A. | 34 | B. | $\sqrt{34}$ | C. | 6 | D. | 3$\sqrt{2}$ |