题目内容
已知集合 的元素全为实数,且满足:若
的元素全为实数,且满足:若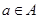 ,则
,则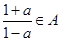 。
。
(1)若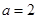 ,求出
,求出 中其它所有元素;
中其它所有元素;
(2)0是不是集合 中的元素?请你设计一个实数
中的元素?请你设计一个实数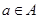 ,再求出
,再求出 中的所有元素?
中的所有元素?
(3)根据(1)(2),你能得出什么结论。
 的元素全为实数,且满足:若
的元素全为实数,且满足:若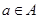 ,则
,则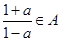 。
。(1)若
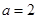 ,求出
,求出 中其它所有元素;
中其它所有元素;(2)0是不是集合
 中的元素?请你设计一个实数
中的元素?请你设计一个实数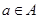 ,再求出
,再求出 中的所有元素?
中的所有元素?(3)根据(1)(2),你能得出什么结论。
(1) 中元素为
中元素为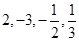 (2)
(2)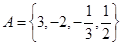 (3)A中的元素为4的倍数
(3)A中的元素为4的倍数
 中元素为
中元素为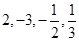 (2)
(2)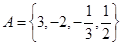 (3)A中的元素为4的倍数
(3)A中的元素为4的倍数本题考查的知识点是元素与集合关系的判断,其中根据已知中若a∈A,则 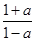
∈A,将已知条件代入进行递推是解答本题的关键,在(3)的解答中易忽略使
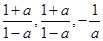 三式均有意义时,对a的限制,而不能得到满分.
三式均有意义时,对a的限制,而不能得到满分.
(1)由已知中若a∈A,则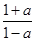 ∈A,
∈A,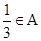 由a=2∈A,可得
由a=2∈A,可得 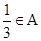 ,再由
,再由
2∈A,进而得到A中的所有元素;
(2)根据已知中若a∈A,则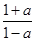 ∈A,令0∈A,可得-1∈A,根据此时
∈A,令0∈A,可得-1∈A,根据此时
中分母为0,式子无意义,即可得到结论;
(3)根据已知中若a∈A,则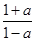 ∈A,结合(1)的结论可得
∈A,结合(1)的结论可得 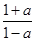 ∈A,而根据(2)的结论,可得要使 三式
∈A,而根据(2)的结论,可得要使 三式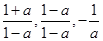 ,均有意义,应有a≠0,a≠±1
,均有意义,应有a≠0,a≠±1
解:(1)由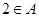 ,则
,则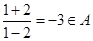 ,又由
,又由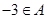 ,得
,得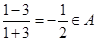 ,再由
,再由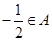
得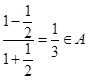 ,而
,而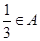 ,得
,得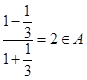 ,故
,故 中元素为
中元素为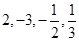 .… 4分
.… 4分
(2) 不是
不是 的元素.若
的元素.若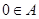 ,则
,则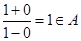 ,而当
,而当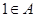 时,
时,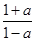 不存在,故0不是
不存在,故0不是 的元素.取
的元素.取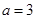 ,可得
,可得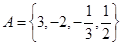 .……………… 8分
.……………… 8分
(3) 猜想:① 中没有元素
中没有元素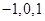 ;②已知A中的一个元素可得其余3个,且每两个互为负倒数.③A中元素个数为4的倍数。………10分
;②已知A中的一个元素可得其余3个,且每两个互为负倒数.③A中元素个数为4的倍数。………10分
①由上题知: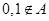 .若
.若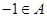 ,则
,则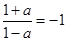 无解.故
无解.故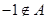 ……12分
……12分
②设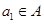 ,则
,则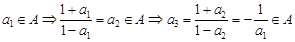
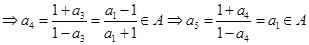 ,
,
且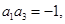
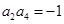 .
.
显然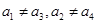 .若
.若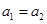 ,则
,则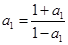 ,得:
,得: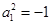 无实数解.
无实数解.
同理,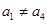 .
.
故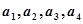 四个互不相等的数.
四个互不相等的数.
故A中的元素为4的倍数……………… 14分
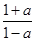
∈A,将已知条件代入进行递推是解答本题的关键,在(3)的解答中易忽略使
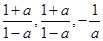 三式均有意义时,对a的限制,而不能得到满分.
三式均有意义时,对a的限制,而不能得到满分.(1)由已知中若a∈A,则
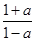 ∈A,
∈A,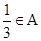 由a=2∈A,可得
由a=2∈A,可得 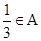 ,再由
,再由 2∈A,进而得到A中的所有元素;
(2)根据已知中若a∈A,则
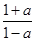 ∈A,令0∈A,可得-1∈A,根据此时
∈A,令0∈A,可得-1∈A,根据此时 中分母为0,式子无意义,即可得到结论;
(3)根据已知中若a∈A,则
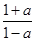 ∈A,结合(1)的结论可得
∈A,结合(1)的结论可得 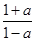 ∈A,而根据(2)的结论,可得要使 三式
∈A,而根据(2)的结论,可得要使 三式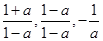 ,均有意义,应有a≠0,a≠±1
,均有意义,应有a≠0,a≠±1解:(1)由
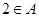 ,则
,则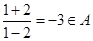 ,又由
,又由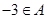 ,得
,得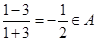 ,再由
,再由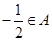
得
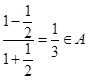 ,而
,而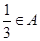 ,得
,得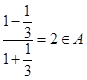 ,故
,故 中元素为
中元素为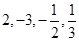 .… 4分
.… 4分(2)
 不是
不是 的元素.若
的元素.若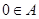 ,则
,则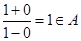 ,而当
,而当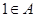 时,
时,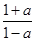 不存在,故0不是
不存在,故0不是 的元素.取
的元素.取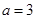 ,可得
,可得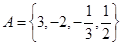 .……………… 8分
.……………… 8分(3) 猜想:①
 中没有元素
中没有元素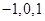 ;②已知A中的一个元素可得其余3个,且每两个互为负倒数.③A中元素个数为4的倍数。………10分
;②已知A中的一个元素可得其余3个,且每两个互为负倒数.③A中元素个数为4的倍数。………10分①由上题知:
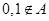 .若
.若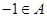 ,则
,则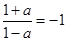 无解.故
无解.故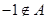 ……12分
……12分②设
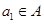 ,则
,则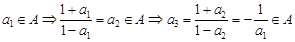
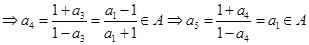 ,
,且
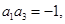
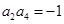 .
.显然
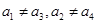 .若
.若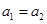 ,则
,则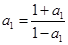 ,得:
,得: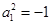 无实数解.
无实数解.同理,
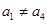 .
.故
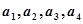 四个互不相等的数.
四个互不相等的数.故A中的元素为4的倍数……………… 14分

练习册系列答案
相关题目
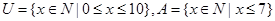 ,则
,则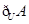 的元素个数( )
的元素个数( )
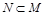

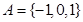 ,则
,则 

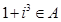

 ,则满足
,则满足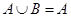 的集合B的个数是( )
的集合B的个数是( ) .设集合
.设集合 ,
,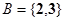 ,则集合
,则集合 的所有元素之和为 ( )
的所有元素之和为 ( )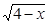 +lg(3
+lg(3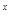 -9)的定义域为A,集合B=
-9)的定义域为A,集合B=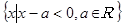 ,
,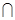 B。
B。 的实数全体
的实数全体 ,定义集合
,定义集合 ,
, 已知
已知 ,则
,则 的子集为
的子集为