题目内容
在宽8米的教室前面有一个长6米的黑板,学生区域CDFE距黑板最近1米,如图,在CE上寻找黑板AB的最大视角点P,AP交CD于Q,区域CPQ为教室黑板的盲区,求此区域面积为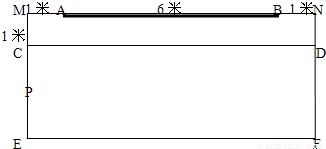
【答案】分析:设PC=x(x≥0),∠BPM=α,∠APM=β,∠BPA=θ(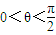 )则tanα=
)则tanα=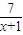 ,
,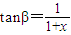 ,而tanθ=tan(α-β)=
,而tanθ=tan(α-β)=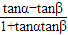 =
=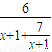 ,结合函数f(x)=x+1+
,结合函数f(x)=x+1+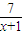 ,(x≥0)的单调性可求f(x)的最小值,从而可求tanθ最大也即θ最大值及相应的CP,在Rt△CPQ中,由tanβ=
,(x≥0)的单调性可求f(x)的最小值,从而可求tanθ最大也即θ最大值及相应的CP,在Rt△CPQ中,由tanβ=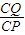 可得CQ=CP•tanβ可求CQ,代入三角形的面积公式S△CPQ=
可得CQ=CP•tanβ可求CQ,代入三角形的面积公式S△CPQ=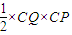 可求
可求
解答:解:设PC=x(x≥0),∠BPM=α,∠APM=β,∠BPA=θ(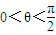 )
)
则tanα=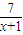 ,
,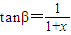
tanθ=tan(α-β)= =
=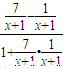 =
=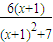 =
=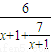
令f(x)=x+1+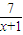 ,(x≥0)则f(x)在[0,
,(x≥0)则f(x)在[0,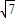 -1]单调递减在,
-1]单调递减在,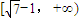 单调递增
单调递增
∴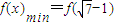 =
=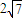 ,此时x+1=
,此时x+1=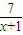 即
即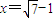 时,函数f(x)有最小值,tanθ最大也即θ最大
时,函数f(x)有最小值,tanθ最大也即θ最大
∴Rt△CPQ中,由tanβ=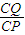 可得CQ=CP•tanβ=
可得CQ=CP•tanβ=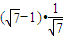 =
=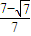
∴S△CPQ=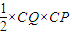 =
=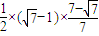 =
=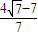
故答案为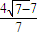

点评:本题主要考查视角的知识,两角差的正切公式及利用函数f(x)=x+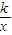 (k>0)的单调性求解函数的最值,属于综合性试题,两角差的正切公式及函数单调性的综合应用是解决本题的关键.
(k>0)的单调性求解函数的最值,属于综合性试题,两角差的正切公式及函数单调性的综合应用是解决本题的关键.
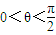 )则tanα=
)则tanα=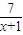 ,
,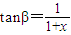 ,而tanθ=tan(α-β)=
,而tanθ=tan(α-β)=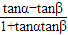 =
=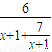 ,结合函数f(x)=x+1+
,结合函数f(x)=x+1+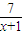 ,(x≥0)的单调性可求f(x)的最小值,从而可求tanθ最大也即θ最大值及相应的CP,在Rt△CPQ中,由tanβ=
,(x≥0)的单调性可求f(x)的最小值,从而可求tanθ最大也即θ最大值及相应的CP,在Rt△CPQ中,由tanβ=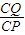 可得CQ=CP•tanβ可求CQ,代入三角形的面积公式S△CPQ=
可得CQ=CP•tanβ可求CQ,代入三角形的面积公式S△CPQ=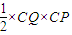 可求
可求解答:解:设PC=x(x≥0),∠BPM=α,∠APM=β,∠BPA=θ(
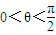 )
)则tanα=
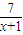 ,
,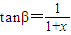
tanθ=tan(α-β)=
 =
=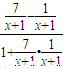 =
=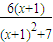 =
=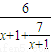
令f(x)=x+1+
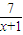 ,(x≥0)则f(x)在[0,
,(x≥0)则f(x)在[0,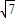 -1]单调递减在,
-1]单调递减在,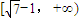 单调递增
单调递增∴
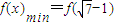 =
=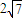 ,此时x+1=
,此时x+1=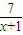 即
即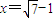 时,函数f(x)有最小值,tanθ最大也即θ最大
时,函数f(x)有最小值,tanθ最大也即θ最大∴Rt△CPQ中,由tanβ=
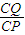 可得CQ=CP•tanβ=
可得CQ=CP•tanβ=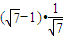 =
=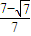
∴S△CPQ=
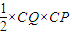 =
=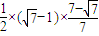 =
=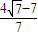
故答案为
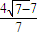

点评:本题主要考查视角的知识,两角差的正切公式及利用函数f(x)=x+
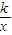 (k>0)的单调性求解函数的最值,属于综合性试题,两角差的正切公式及函数单调性的综合应用是解决本题的关键.
(k>0)的单调性求解函数的最值,属于综合性试题,两角差的正切公式及函数单调性的综合应用是解决本题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
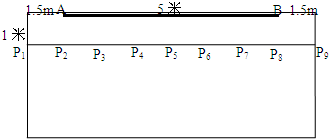 在宽为8米的教室前面有一个长为5米的黑板,距离黑板1米,间隔1米的学生Pi,i=1,2,…,9,如图,当视角∠APiB小于45°时,该学生处在教室黑板盲区,此类学生是
在宽为8米的教室前面有一个长为5米的黑板,距离黑板1米,间隔1米的学生Pi,i=1,2,…,9,如图,当视角∠APiB小于45°时,该学生处在教室黑板盲区,此类学生是

