Question

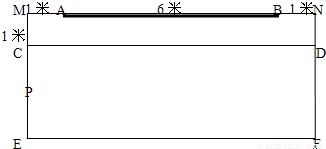
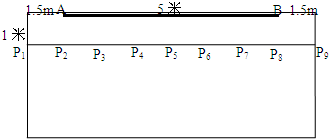在宽为8米的教室前面有一个长为5米的黑板，距离黑板1米，间隔1米的学生P_i，i=1，2，…，9，如图，当视角∠AP_iB小于45°时，该学生处在教室黑板盲区，此类学生是

P₁，P₉

．

Answer 1

分析：利用几何性质直接判断P₁，P₉学生处在教室黑板盲区，通过余弦定理求出∠AP₂B的大小，利用对称性判断P₈是否是盲区．

解答：解：如图连接AP₁，BP₁，AP₂，BP₂，
由图象可知∠AP₁P₂＜45°，所以P₁，P₉学生处在教室黑板盲区，
AP₂=

1+( 1 2 )2

=

5

2

，BP₂=

1+( 11 2 )2

=

5 5

2

，
由余弦定理可知，cos∠AP₂B=

( 5 2 )2+( 5 5 2 )2-52

2× 5 2 × 5 5 2

=

3

5

，
∵

1

2

＜

3

5

＜

2

2

，∴60°＞∠AP₂B＞45°，
由对称性可知∠AP₈B＞45°，
其它位置显然不是盲区，
在教室黑板盲区位置，此类学生是 P₁，P₉
故答案为：P₁，P₉．

点评：本题考查分析问题解决问题，余弦定理的应用，考查计算能力，注意几何性质的应用．