题目内容
已知平面α的法向量是(2,3,-1),平面β的法向量是(4,λ,-2),若α∥β,则λ的值为
6
6
.分析:根据已知条件结合面面平行其法向量必然平行,可得存在实数μ使得,(2,3,-1)=(4μ,λμ,-2μ),根据坐标对应相等构造方程,可求出λ值.
解答:解:∵α∥β,且平面α的法向量是
=(2,3,-1),平面β的法向量是
=(4,λ,-2),
∴
∥
即存在实数μ使得,
=μ
即(2,3,-1)=(4μ,λμ,-2μ),
解得μ=
,λ=6
故答案为:6
| m |
| n |
∴
| m |
| n |
即存在实数μ使得,
| m |
| n |
即(2,3,-1)=(4μ,λμ,-2μ),
解得μ=
| 1 |
| 2 |
故答案为:6
点评:本题考查的知识点是向量法证平行,其中根据两个平面平行,得到两个平面的两个法向量也平行是解答的关键.

练习册系列答案
相关题目
 ,则
,则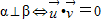 ;
; ;
; .
.