题目内容
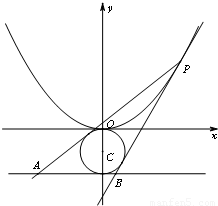
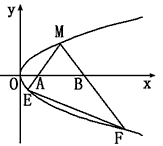
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB,
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程。
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程。
解:(1)设M(y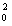 ,y0),直线ME的斜率为k(k>0),
,y0),直线ME的斜率为k(k>0),
则直线MF的斜率为-k,
∴直线ME的方程为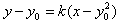 ,
,
∴由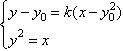 ,消x得
,消x得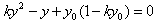 ,
,
解得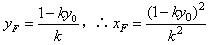 ,
,
∴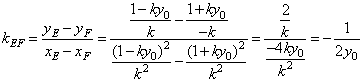 (定值),
(定值),
所以直线EF的斜率为定值;
(2)当∠EMF=90°时,∠MAB=45°,所以k=1,
∴直线ME的方程为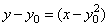 ,
,
有 ,
,
同理可得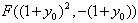 ,
,
设重心G(x, y),
则有 ,
,
消去参数y0得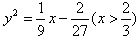 。
。
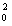 ,y0),直线ME的斜率为k(k>0),
,y0),直线ME的斜率为k(k>0),则直线MF的斜率为-k,
∴直线ME的方程为
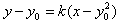 ,
,∴由
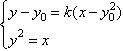 ,消x得
,消x得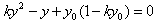 ,
,解得
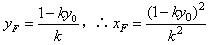 ,
,∴
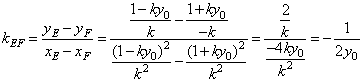 (定值),
(定值),所以直线EF的斜率为定值;
(2)当∠EMF=90°时,∠MAB=45°,所以k=1,
∴直线ME的方程为
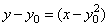 ,
,有
 ,
,同理可得
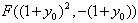 ,
,设重心G(x, y),
则有
 ,
,消去参数y0得
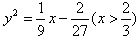 。
。 
练习册系列答案
相关题目
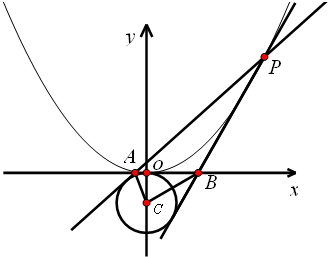 已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2
已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2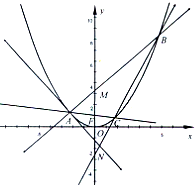 如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N. (2012•浙江模拟)已知抛物线x2=4y.
(2012•浙江模拟)已知抛物线x2=4y.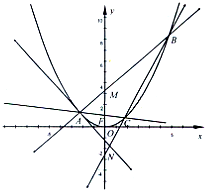 (2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
(2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.