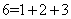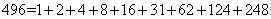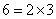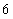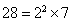题目内容
所有真约数(除本身之外的正约数)的和等于它本身的正整数叫做完全数.
如:6=1+2+3;28=1+2+4+7+14;496=1+2+4+8+16+31+62+124+248.
已经证明:若2n-1是质数,则2n-1(2n-1)是完全数,n∈N*.请写出一个四位完全数 ;又6=2×3,所以6的所有正约数之和可表示为(1+2)•(1+3);28=22×7,所以28的所有正约数之和可表示为(1+2+22)•(1+7);
按此规律,496的所有正约数之和可表示为 .
如:6=1+2+3;28=1+2+4+7+14;496=1+2+4+8+16+31+62+124+248.
已经证明:若2n-1是质数,则2n-1(2n-1)是完全数,n∈N*.请写出一个四位完全数
按此规律,496的所有正约数之和可表示为
分析:利用2n-1是质数,2n-1(2n-1)是完全数,令n=7,可得结论;由496=24×31,可得496的所有正约数之和.
解答:解:∵2n-1是质数,2n-1(2n-1)是完全数,
∴令n=7,可得一个四位完全数为64×(127-1)=8128;
∵496=24×31,∴496的所有正约数之和可表示为(1+2+22+23+24)•(1+31).
故答案为:8128;(1+2+22+23+24)•(1+31).
∴令n=7,可得一个四位完全数为64×(127-1)=8128;
∵496=24×31,∴496的所有正约数之和可表示为(1+2+22+23+24)•(1+31).
故答案为:8128;(1+2+22+23+24)•(1+31).
点评:本题考查合情推理,考查学生分析解决问题的能力,正确理解新定义是关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
 如右图述阵称为“森德拉姆筛”,记第i行第j列的数为Aij,对任意正整数为Aij,必有正整数C使得Aij+C为合数(合数的定义是:合数是除了1和它本身还能被其他的正整数整除的正整数,除2之外的偶数都是合数),则这样的C可以是( )
如右图述阵称为“森德拉姆筛”,记第i行第j列的数为Aij,对任意正整数为Aij,必有正整数C使得Aij+C为合数(合数的定义是:合数是除了1和它本身还能被其他的正整数整除的正整数,除2之外的偶数都是合数),则这样的C可以是( )