题目内容
甲、乙两同学进行投篮比赛,每一局每人各投两次球,规定进球数多者该局获胜,进球数相同则为平局.已知甲每次投进的概率为
,乙每次投进的概率为
,甲、乙之间的投篮相互独立.
(1)求一局比赛甲进两球获胜的概率;
(2)求一局比赛的结果不是平局的概率.
| 2 |
| 3 |
| 1 |
| 2 |
(1)求一局比赛甲进两球获胜的概率;
(2)求一局比赛的结果不是平局的概率.
分析:(1)设“一局比赛甲进两球获胜”为事件A,则P(A)=(
)2•[(
)2+
•(
)2,运算求得结果.
(2)设“一局比赛出现平局”为事件B,则B包括“甲乙都进2个球”,“甲乙都进1个球”,“甲乙都进0个球”三种情况,求出每种情况的概率,相加即得P(B),再根据 P(
)=1-P(B) 求得结果.
| 2 |
| 3 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 2 |
(2)设“一局比赛出现平局”为事件B,则B包括“甲乙都进2个球”,“甲乙都进1个球”,“甲乙都进0个球”三种情况,求出每种情况的概率,相加即得P(B),再根据 P(
. |
| B |
解答:解:(1)设“一局比赛甲进两球获胜”为事件A,
则P(A)=(
)2•[(
)2+
•(
)2=
. …(6分)
(2)设“一局比赛出现平局”为事件B,则事件B包括“甲乙都进2个球”,“甲乙都进1个球”,“甲乙都进0个球”,
三种情况.
则P(B)=(
)2•(
)2+
•
•
•
•(
)2+(
)2•(
)2=
.…(10分)
所以 P(
)=1-P(B),即一局比赛的结果不是平局的概率为
.…(12分)
则P(A)=(
| 2 |
| 3 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)设“一局比赛出现平局”为事件B,则事件B包括“甲乙都进2个球”,“甲乙都进1个球”,“甲乙都进0个球”,
三种情况.
则P(B)=(
| 2 |
| 3 |
| 1 |
| 2 |
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 13 |
| 36 |
所以 P(
. |
| B |
| 23 |
| 36 |
点评:本题主要考查互斥事件的概率加法公式,相互独立事件的概率乘法公式,属于基础题.

练习册系列答案
相关题目
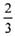 ,乙每次投进的概率为
,乙每次投进的概率为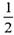 ,甲、乙之间的投篮相互独立.
,甲、乙之间的投篮相互独立. ,乙每次投进的概率为
,乙每次投进的概率为 ,甲、乙之间的投篮相互独立.
,甲、乙之间的投篮相互独立.