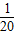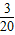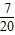题目内容
某校高二（1）班甲、乙两同学进行投篮比赛，他们进球的概率分别是
和
，现甲、乙各投篮一次，恰有一人投进球的概率是（ ）
| 3 |
| 4 |
| 4 |
| 5 |
分析：利用相互独立事件的概率乘法公式求得 甲投进而乙没有投进的概率，以及乙投进而甲没有投进的概率，相加即得所求．
解答：解：甲投进而乙没有投进的概率为
(1-
)=
，乙投进而甲没有投进的概率为 （1-
）•
=
，
故甲、乙各投篮一次，恰有一人投进球的概率是
+
=
，
故选D．
| 3 |
| 4 |
| 4 |
| 5 |
| 3 |
| 20 |
| 3 |
| 4 |
| 4 |
| 5 |
| 1 |
| 5 |
故甲、乙各投篮一次，恰有一人投进球的概率是
| 3 |
| 20 |
| 1 |
| 5 |
| 7 |
| 20 |
故选D．
点评：本题主要考查相互独立事件的概率乘法公式的应用，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
an，数列{bn}的前n项和为Sn，求使sn＋n·2n+1＞50成立的正整数n的最小值．
和
，现甲、乙各投篮一次，恰有一人投进球的概率是（ ）
