题目内容
【题目】矩阵乘法运算![]() 的几何意义为平面上的点
的几何意义为平面上的点![]() 在矩阵
在矩阵![]() 的作用下变换成点
的作用下变换成点![]() ,记
,记![]() ,且
,且![]() .
.
(1)若平面上的点![]() 在矩阵
在矩阵![]() 的作用下变换成点
的作用下变换成点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若平面上相异的两点![]() 、
、![]() 在矩阵
在矩阵![]() 的作用下,分别变换为点
的作用下,分别变换为点![]() 、
、![]() ,求证:若点
,求证:若点![]() 为线段
为线段![]() 上的点,则点
上的点,则点![]() 在
在![]() 的作用下的点
的作用下的点![]() 在线段
在线段![]() 上;
上;
(3)已知△![]() 的顶点坐标为
的顶点坐标为![]() 、
、![]() 、
、![]() ,且△
,且△![]() 在矩阵
在矩阵 作用下变换成△
作用下变换成△![]() ,记△
,记△![]() 与△
与△![]() 的面积分别为
的面积分别为![]() 与
与![]() ,求
,求![]() 的值,并写出一般情况(三角形形状一般化且变换矩阵一般化)下
的值,并写出一般情况(三角形形状一般化且变换矩阵一般化)下![]() 与
与![]() 的关系(不要求证明).
的关系(不要求证明).
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() ,若变化矩阵为
,若变化矩阵为![]() ,则
,则![]() .
.
【解析】
(1)直接根据矩阵变换的计算,可得点的坐标;
(2)先求变换后![]() 的坐标,再利用斜率相等,即可证得
的坐标,再利用斜率相等,即可证得![]() 共线;
共线;
(3)求出点![]() ,
,![]() ,
,![]() ,利用行列式计算三角形面积即可.
,利用行列式计算三角形面积即可.
(1)设![]() ,则
,则![]() ,
,
∴![]() 解得:
解得:![]() ,
,
∴![]() .
.
(2)设![]() ,
,![]() ,
,
∵![]() 三点共线,∴
三点共线,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∵ ,
,
 ,
,
∴![]()
![]() ,∴点
,∴点![]() 在
在![]() 的作用下的点
的作用下的点![]() 在线段
在线段![]() 上.
上.
(3)∵ ,
, ,
,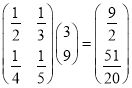 ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴
![]()
![]()
![]() .
.
∴![]() .
.
若矩阵为![]() ,则
,则![]() .
.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目




