题目内容
已知正方形ABCD内接于半径为2、球心为O的球的截面小圆O',若小圆O'的半径为
,球面上五点S、A、B、C、D构成正四棱锥S-ABCD,且点S、O在平面ABCD异侧,则点S、C在该球面上的球面距离为
π
π.
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
分析:因为正四棱锥的顶点在球面上,正四棱锥的高所在的直线经过球的直径,如图,在直角三角形OCO′求出球心角∠COO′,就可以求出S、C的球面距离.
解答: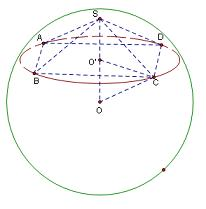 解:正四棱锥S-ABCD中,如图,
解:正四棱锥S-ABCD中,如图,
正方形ABCD内接于半径为2、球心为O的球的截面小圆O',
连接OC,O′C,在直角三角形O′OC中,
小圆O'的半径O′C=
,球的半径OC=2,
得sin∠O′OC=
=
,∴∠O′OC=
,
∴S、C两点间的球面距离为
×OC=
π,
故答案为:
π.
 解:正四棱锥S-ABCD中,如图,
解:正四棱锥S-ABCD中,如图,正方形ABCD内接于半径为2、球心为O的球的截面小圆O',
连接OC,O′C,在直角三角形O′OC中,
小圆O'的半径O′C=
| 3 |
得sin∠O′OC=
| O′C |
| OC |
| ||
| 2 |
| π |
| 3 |
∴S、C两点间的球面距离为
| π |
| 3 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查学生的空间想象能力,以及学生对球的结构认识,是基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知正方形ABCD的边长为6,空间有一点M(不在平面ABCD内)满足|MA|+|MB|=10,则三棱锥A-BCM的体积的最大值是( )
| A、48 | B、36 | C、30 | D、24 |
已知正方形ABCD的边长为2,则该正方形内的点到正方形的顶点A、B、C、D的距离均不小于1的概率是
( )
( )
A、
| ||
B、1-
| ||
C、1-
| ||
D、1-
|
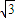 ,球面上五点S、A、B、C、D构成正四棱锥S-ABCD,且点S、O在平面ABCD异侧,则点S、C在该球面上的球面距离为 .
,球面上五点S、A、B、C、D构成正四棱锥S-ABCD,且点S、O在平面ABCD异侧,则点S、C在该球面上的球面距离为 .