题目内容
某公司承担了每天至少搬运280吨水泥的任务,已知该公司有6辆A型卡车和8辆B型卡车.又已知A型卡车每天每辆的运载量为30吨,成本费为0.9千元;B型卡车每天每辆的运载量为40吨,成本费为1千元.
(1)如果你是公司的经理,为使公司所花的成本费最小,每天应派出A型卡车、B型卡车各多少辆?
(2)在(1)的所求区域内,求目标函数 的最大值和最小值.
的最大值和最小值.
(1) 型卡车0辆,
型卡车0辆,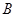 型卡车
型卡车 辆;(2)在
辆;(2)在 处取最大值
处取最大值 ,在
,在 处取最小值
处取最小值 .
.
解析试题分析:(1)根据题意可得出关于A型卡车、B型卡车的一组限制条件 ,由目标函数
,由目标函数 化简得
化简得 ,平移直线可得当直线经过点
,平移直线可得当直线经过点 时,直线在
时,直线在 轴上的截距最小,即
轴上的截距最小,即 取最小值,为
取最小值,为 ;(2)由目标函数
;(2)由目标函数 可联想到两点确定的斜率坐标公式
可联想到两点确定的斜率坐标公式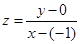 ,这是两点
,这是两点 之间的斜率,结合图象不难发现,平移直线可得当直线过点
之间的斜率,结合图象不难发现,平移直线可得当直线过点 处取最大值
处取最大值 ,过点
,过点 处取最小值
处取最小值 .
.
试题解析:(1)设公司每天派出 型卡车
型卡车 辆,
辆,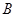 型卡车
型卡车 辆,公司所花的成本费为
辆,公司所花的成本费为 千元,根据题意,得
千元,根据题意,得 ,目标函数
,目标函数 ,作出该不等式组表示的可行域,如下图.
,作出该不等式组表示的可行域,如下图.
考虑 ,变形为
,变形为 ,这是以
,这是以 为斜率,
为斜率, 为
为 轴上的截距的平行直线族.
轴上的截距的平行直线族.
经过可行域,平行移动直线,当直线经过点 时,直线在
时,直线在 轴上的截距最小,即
轴上的截距最小,即 取最小值,为
取最小值,为
答:公司每天派出 型卡车0辆,
型卡车0辆,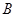 型卡车
型卡车 辆时,所花的成本费最低,为
辆时,所花的成本费最低,为 千元.
千元.
(2)在 处取最大值
处取最大值 ,在
,在 处取最小值
处取最小值 .
.
考点:1.简单的线性规划;2.直线方程;3.两点的斜率坐标公式

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大。已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
| 资 金 | 每台单位产品所需资金(百元) | 月资金供应量 (百元) | |
| 空调机 | 洗衣机 | ||
| 成 本 | 30 | 20 | 300 |
| 劳动力(工资) | 5 | 10 | 110 |
| 每台产品利润 | 6 | 8 | |
已知: ,
, ,那么下列不等式成立的是( )
,那么下列不等式成立的是( )
A. | B. |
C. | D.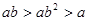 |
若1<x<10,下面不等式中正确的是 ( )
| A.(lgx)2<lgx2<lg(lgx) |
| B.lgx2<(lgx)2<lg(lgx) |
| C.(lgx)2<lg(lgx)<lgx2 |
| D.lg(lgx)<(lgx)2<lgx2 |
 ,其中,角
,其中,角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点 ,且
,且 .
. 点的坐标为(-
点的坐标为(- ),求
),求 的值;
的值;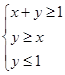 上的一个动点,试确定角
上的一个动点,试确定角 ,则
,则 的最小值为__________ -
的最小值为__________ -