题目内容
（2011•安徽模拟）已知x、y∈R，若集合A={（x，y）|x2+y2=1}，集合B={（x，y）|kx-y-2≤0}，则“k=
”是“A∪B=B”的（ ）
| 3 |
分析：因为集合A和B均为点的集合，所以可以考虑用数形结合求解．
解答：解：集合A为单位圆上的点，
集合B表示恒过（0，-2）点的直线一侧的区域，
若“A∪B=B”，则A⊆B，如下图所示：
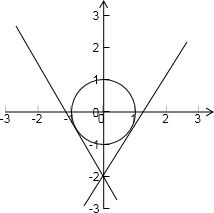
当直线kx-y-2=0与圆相切时，k=±
，故k的范围为[-
，
]，
∴“k=
”⇒“A∪B=B”，
“A∪B=B”⇒k∈[-
，
]，
故“k=
”是“A∪B=B”充分不必要条件．
故选B．
集合B表示恒过（0，-2）点的直线一侧的区域，
若“A∪B=B”，则A⊆B，如下图所示：
当直线kx-y-2=0与圆相切时，k=±
| 3 |
| 3 |
| 3 |
∴“k=
| 3 |
“A∪B=B”⇒k∈[-
| 3 |
| 3 |
故“k=
| 3 |
故选B．
点评：本题考查集合间的相互关系的应用，是基础题．解题时要认真审题，仔细解答，注意数形结合思想的运用．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目