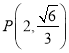题目内容
【题目】已知函数
（
且
）在
上恒正，则实数
的取值范围为（ ）
A.
B.
C.
D.
【答案】B
【解析】
由题意得当0＜a＜1时，0＜ax2﹣x+
＜1在[1，3]上恒成立，当a＞1时，ax2﹣x+＞1在[1，3]上恒成立，然后利用分离法可求出a的取值范围．
当0＜a＜1时，函数f（x）＝loga（ax2﹣x+）（a＞0且a≠1）在[1，3]上恒正，即0＜ax2﹣x+＜1在[1，3]上恒成立，
∴﹣
＜a＜，而（﹣）max＝，（）min＝[
]min＝
，∴＜a＜不可能，故舍去；
当a＞1时，函数f（x）＝loga（ax2﹣x+）（a＞0且a≠1）在[1，3]上恒正则ax2﹣x+＞1在[1，3]上恒成立，
即a＞（）max＝[]max＝
，故实数a的取值范围为
故选：B
练习册系列答案
阅读快车系列答案
相关题目
【题目】孔子曰：温故而知新.数学学科的学习也是如此.为了调查数学成绩与及时复习之间的关系，某校志愿者展开了积极的调查活动：从高三年级640名学生中按系统抽样抽取40名学生进行问卷调查，所得信息如下：
数学成绩优秀（人数） | 数学成绩合格（人数） | |
及时复习（人数） | 20 | 4 |
不及时复习（人数） | 10 | 6 |
（1）张军是640名学生中的一名，他被抽中进行问卷调查的概率是多少（用分数作答）；
（2）根据以上数据，运用独立性检验的基本思想，研究数学成绩与及时复习的相关性.
参考公式：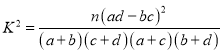
，其中
为样本容量
临界值表：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
