题目内容
3. 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥面ABCD,PD=2,PB与面ABCD所成的角的大小为30°.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥面ABCD,PD=2,PB与面ABCD所成的角的大小为30°.(1)若E是PD的中点,求异面直线PA与BE所成角的大小;
(2)求△PAD以PA为轴旋转所成几何体的体积.
分析 (1)如图所示,连接BD,取AD的中点F,连接EF,BF.利用三角形中位线定理可得∠BEF或其补角是异面直线PA与BE所成角.由于侧棱PD⊥面ABCD,PB与面ABCD所成的角的大小为30°.可得∠PBD=30°.可得PB,BD.AB.BF,BE,EF.在△BEF中,利用余弦定理即可得出cos∠BEF.
(2)如图所示,作DO⊥PA,垂足为O,利用直角三角形的边角关系可得PA,OD.利用△PAD以PA为轴旋转所成几何体的体积V=$\frac{1}{3}×πO{D}^{2}×PA$即可得出.
解答 解:(1)如图所示,连接BD,取AD的中点F,连接EF,BF.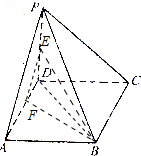
∴EF$\underset{∥}{=}\frac{1}{2}PA$,
∴∠BEF或其补角是异面直线PA与BE所成角.
∵侧棱PD⊥面ABCD,PB与面ABCD所成的角的大小为30°.
∴∠PBD=30°.
∵PD=2,∴PB=4,BD=2$\sqrt{3}$.
∴$2A{B}^{2}=(2\sqrt{3})^{2}$,
解得AB=$\sqrt{6}$.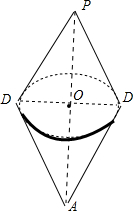
∴$BF=\sqrt{A{B}^{2}+A{F}^{2}}$=$\frac{\sqrt{30}}{2}$.
又BE=$\sqrt{D{E}^{2}+B{D}^{2}}$=$\sqrt{13}$.
$EF=\sqrt{D{F}^{2}+D{E}^{2}}$=$\frac{\sqrt{10}}{2}$.
在△BEF中,cos∠BEF=$\frac{B{E}^{2}+E{F}^{2}-B{F}^{2}}{2BE•EF}$=$\frac{13+\frac{10}{4}-\frac{30}{4}}{2×\sqrt{13}×\frac{\sqrt{10}}{2}}$=$\frac{4\sqrt{130}}{65}$.
∴∠BEF=arccos$\frac{4\sqrt{130}}{65}$.
(2)如图所示,
作DO⊥PA,垂足为O,
∵PA=$\sqrt{P{D}^{2}+A{D}^{2}}$=$\sqrt{10}$,
OD=$\frac{PD•AD}{PA}$=$\frac{2\sqrt{6}}{\sqrt{10}}$=$\frac{2\sqrt{15}}{5}$.
∴△PAD以PA为轴旋转所成几何体的体积V=$\frac{1}{3}×πO{D}^{2}×PA$=$\frac{1}{3}×π×\frac{4×3}{5}$×$\sqrt{10}$=$\frac{4\sqrt{10}π}{5}$.
点评 本题考查了线面垂直的性质定理、线面角、异面直线所成的角、余弦定理、直角三角形的边角关系、圆锥的体积计算公式,考查了空间想象能力、推理能力与计算能力,属于中档题.

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案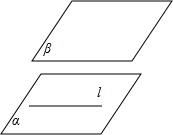
| A. | α∩β=l | B. | α∥β,l∈α | C. | l∥β,l?α | D. | α∥β,l?α |