Question

已知不等式组

x≥0，y≥0 2x+y-1≤0

表示平面区域D，现在往抛物线y=-x²+x+2与x轴围成的封闭区域内随机地抛掷一小颗粒，则该颗粒落到区域D中的概率为（　　）

• A、

  1

  9

• B、

  1

  18

• C、

  1

  3

• D、

  1

  6

Answer 1

分析：根据积分的知识可得先求y=-x²+x+2与x轴围成的封闭区域为曲面MEN，的面积，然后根据线性规划的知识作出平面区域D，并求面积，最后代入几何概率的计算公式可求．

解答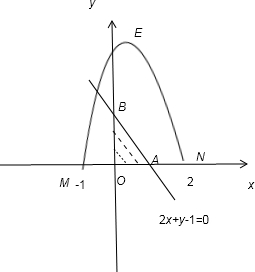：解：根据积分的知识可得，y=-x²+x+2与x轴围成的封闭区域为曲面MEN，面积

∫

2 -1

(-x2+x+2)dx=-

1

3

x3+

1

2

x2+2x

|

2 -1

=

9

2

等式组

x≥0，y≥0 2x+y-1≤0

表示平面区域D即为△AOB，其面积为

1

4

根据几何概率的计算公式可得P=

1

18

故选：C

点评：本题主要考查了利用积分求解曲面的面积，还考查了几何概率的计算公式的应用，属于基础试题．