题目内容
(2012•佛山二模)已知不等式组
表示的平面区域为Ω,其中k≥0,则当Ω的面积最小时的k为
|
1
1
.分析:先画出不等式组
所表示的平面区域,然后表示出图形的面积,最后利用基本不等式求出面积的最值即可.
|
解答: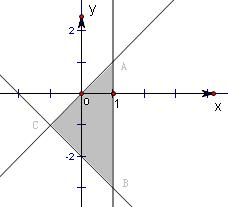 解:画出不等式组
解:画出不等式组
所表示的平面区域,如图.
A(1,k),B(1,-3),C(-
,-
)
根据题意可知不等式组
所表示的平面区域为三角形ABC,其面积等于:
S=
×AB×h
=
(k+3)(1+
)
=
(k+1+2)(1+
)
=
(4+k+1+
)
≥
(4+4)=4,当且仅当k+1=
时取等号,即k=1.
故答案为:1.
 解:画出不等式组
解:画出不等式组
|
A(1,k),B(1,-3),C(-
| 2 |
| k+1 |
| 2k |
| k+1 |
根据题意可知不等式组
|
S=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| k+1 |
=
| 1 |
| 2 |
| 2 |
| k+1 |
=
| 1 |
| 2 |
| 4 |
| k+1 |
≥
| 1 |
| 2 |
| 4 |
| k+1 |
故答案为:1.
点评:本题考查简单的线性规划,以及利用基本不等式等知识求最值问题,是中档题.

练习册系列答案
相关题目
 (2012•佛山二模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
(2012•佛山二模)空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重: (2012•佛山二模)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
(2012•佛山二模)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )