题目内容
若函数y=ax3+(2-a)x在R上恒为增函数,则
- A.a∈(0,2]
- B.a∈(0,2)∪(2,∞)
- C.a∈(0,2)
- D.a∈[0,2]
D
分析:利用导数与函数单调性的关系转化为f′(x)≥0恒成立处理.
解答:因为函数y=ax3+(2-a)x在R上为增函数,所以y′=3ax2+2-a≥0在R上恒成立,
①当a=0时,显然成立;②当a>0时,即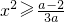 恒成立,此时
恒成立,此时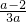 ≤0,所以0<a≤2;
≤0,所以0<a≤2;
③当a<0时,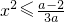 ,不恒成立.
,不恒成立.
综上,a的取值范围为[0,2].
故选D
点评:此题考查导函数与函数单调性的关系,可导函数f(x)在某区间上单调递增的充要条件是f′(x)≥0(不恒为0).
分析:利用导数与函数单调性的关系转化为f′(x)≥0恒成立处理.
解答:因为函数y=ax3+(2-a)x在R上为增函数,所以y′=3ax2+2-a≥0在R上恒成立,
①当a=0时,显然成立;②当a>0时,即
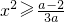 恒成立,此时
恒成立,此时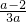 ≤0,所以0<a≤2;
≤0,所以0<a≤2;③当a<0时,
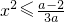 ,不恒成立.
,不恒成立.综上,a的取值范围为[0,2].
故选D
点评:此题考查导函数与函数单调性的关系,可导函数f(x)在某区间上单调递增的充要条件是f′(x)≥0(不恒为0).

练习册系列答案
相关题目