题目内容
设椭圆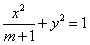 的两个焦点是F1(-c,0),F2(c,0)(c>0),且椭圆上存在点P,使得直线PF1与直线PF2垂直,
的两个焦点是F1(-c,0),F2(c,0)(c>0),且椭圆上存在点P,使得直线PF1与直线PF2垂直,
(Ⅰ)求实数m的取值范围;
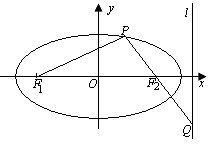
(Ⅱ)设l是相应于焦点F2的准线,直线PF2与l相交于点Q。若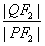 =2-
=2-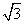 ,求直线PF2的方程。
,求直线PF2的方程。
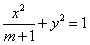 的两个焦点是F1(-c,0),F2(c,0)(c>0),且椭圆上存在点P,使得直线PF1与直线PF2垂直,
的两个焦点是F1(-c,0),F2(c,0)(c>0),且椭圆上存在点P,使得直线PF1与直线PF2垂直,(Ⅰ)求实数m的取值范围;
(Ⅱ)设l是相应于焦点F2的准线,直线PF2与l相交于点Q。若
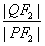 =2-
=2-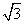 ,求直线PF2的方程。
,求直线PF2的方程。 |
解:(Ⅰ)∵直线PF1⊥直线PF2, |
 |
| (Ⅱ)设P(x0,y0),Q(x1,y1), ∵准线l的方程为: 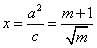 , ,∴x1=  , , ∵ 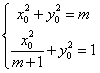 , , ∴  , , ∵ 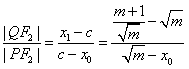 , ① , ① 将 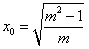 代入①, 代入①,化简得: 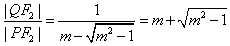 , ,由题设 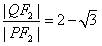 , ,得: 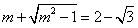 ,无解; ,无解;将 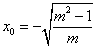 代入①, 代入①,化简得:  , ,由题设 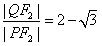 , ,得: 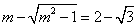 ,解得m=2, ,解得m=2,从而 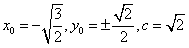 , ,得到直线PF2的方程为: 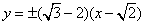 。 。 |
 |

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
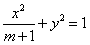 有交点,即
有交点,即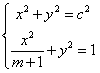 有解,
有解,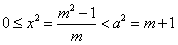 ,
,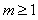 。
。 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.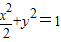 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.