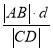题目内容
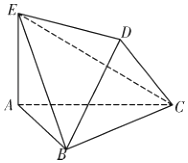
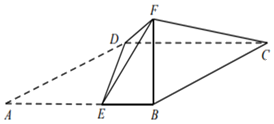
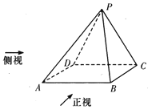
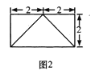
【题目】如图，四棱柱
中，
平面
，四边形为平行四边形，
，
．
（1）若
，求证：
平面
；
（2）若
，
，求二面角
的余弦值．
【答案】（1）见解析；（2）
．
【解析】
（1）连接
，交
于点
，可证得四边形
为平行四边形，从而得到
，根据线面平行的判定定理可证得结论；
（2）在
中，由余弦定理可求得
，进而得到
；由线面垂直的性质和判定定理可证得
平面
；作
，可知
即为所求二面角的平面角，由长度关系可求得结果.
（1）证明：如图所示，连接，交于点，连接
．
，
，
，
，
四边形为平行四边形，
，
平面
，
平面，
平面.
（2）解：
四边形
为平行四边形，
，
，
，
.
设
，由余弦定理得：
，解得：
，
，
，
又
平面，
，
平面，
又
平面，
，
平面，
，
平面
作，垂足为
，连接
，则
，
为二面角
的平面角.
，
，
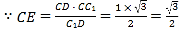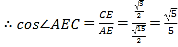，即二面角的余弦值为.
【题目】某县共有户籍人口60万，经统计，该县60岁及以上、百岁以下的人口占比
，百岁及以上老人15人.现从该县60岁及以上、百岁以下的老人中随机抽取230人，得到如下频数分布表：
年龄段（岁） |
|
|
|
|
人数（人） | 125 | 75 | 25 | 5 |
（1）从样本中70岁及以上老人中，采用分层抽样的方法抽取21人，进一步了解他们的生活状况，则80岁及以上老人应抽多少人？
（2）从（1）中所抽取的80岁及以上老人中，再随机抽取2人，求抽到90岁及以上老人的概率；
（3）该县按省委办公厅、省人民政府办公厅《关于加强新时期老年人优待服务工作的意见》精神，制定如下老年人生活补贴措施，由省、市、县三级财政分级拨款：
①本县户籍60岁及以上居民，按城乡居民养老保险实施办法每月领取55元基本养老金；
②本县户籍80岁及以上老年人额外享受高龄老人生活补贴；
（a）百岁及以上老年人，每人每月发放345元的生活补贴；
（b）90岁及以上、百岁以下老年人，每人每月发放200元的生活补贴；
（c）80岁及以上、90岁以下老年人，每人每月发放100元的生活补贴.
试估计政府执行此项补贴措施的年度预算.
