Question

以下命题正确的是

 

．
①把函数y=3sin(2x+

π

3

)的图象向右平移

π

6

个单位，得到y=3sin2x的图象；
②一平面内两条曲线的方程分别是f₁（x，y）=0，f₂（x，y）=0，它们的交点是P（x₀，y₀），则方程f₁（x，y）+f₂（x，y）=0表示的曲线经过点P；
③ABCD为长方形，AB=2，BC=1，O为AB的中点，在长方形ABCD内随机取一点，取得的点到O的距离大于1的概率为1-

π

2

；
④若等差数列{a_n}前n项为S_n，则三点（10，

S10

10

），（100，

S100

100

），（110，

S110

110

）共线．

Answer 1

分析：①中图象的平移符合左加右减，注意平移的数要加在x上；②点在曲线上，点的坐标满足方程；
③为几何概型，转化为面积之比；④由等差数列前n项和公示为关于n的二次函数可得．

解答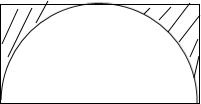：解：①把函数y=3sin(2x+

π

3

)的图象向右平移

π

6

个单位，
得到y=3sin（2（x-

π

6

）+

π

3

）=3sin2x，结论正确；
②一平面内两条曲线的方程分别是f₁（x，y）=0，f₂（x，y）=0，
它们的交点是P（x₀，y₀），可得f₁（x₀，y₀）=0，f₂（x₀，y₀）=0
∴f₁（x₀，y₀）+f₂（x₀，y₀）=0，
∴方程f₁（x，y）+f₂（x，y）=0表示的曲线经过点P正确；
③所求概率为阴影部分和矩形面积之比，即为

2- π 2

2

=1-

π

4

，结论错误；
④若等差数列{a_n}的前n项和s_n=An²+Bn，则

sn

n

=An+B为一次型函数，图象为一条直线，故结论正确；
故答案为：①②④

点评：本题以命题的真假判断为载体考查函数图形的平移、曲线与方程、几何概型、等差数列等知识，考查面广．