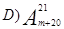题目内容
(本题12分,)有6名同学站成一排,求:
(1)甲不站排头也不站排尾有多少种不同的排法:
(2)甲、乙、丙不相邻有多少种不同的排法.(均须先列式再用数字作答)
(1)甲不站排头也不站排尾有多少种不同的排法:
(2)甲、乙、丙不相邻有多少种不同的排法.(均须先列式再用数字作答)
(1)A41A55=480种;(2)A33A43=144种.
站队问题是排列组合中的典型问题,解题时要先排限制条件多的元素,把限制条件比较多的元素排列后,再排没有限制条件的元素,最后要用分步计数原理得到结果.
(1)甲不站排头也不站排尾,甲要站在除去排头和排尾的四个位置,余下的五个位置使五个元素全排列,根据分步计数原理得到结果.
(2)甲、乙、丙不相邻,可以采用甲,乙和丙插空法,首先排列除去甲,乙和丙之外的三个人,有A33种结果,再在三个元素形成的四个空中排列3个元素,共有A43,根据分步计数原理得到结果.
解:
(1)∵甲不站排头也不站排尾,∴甲要站在除去排头和排尾的四个位置,余下的五个位置使五个元素全排列,根据分步计数原理知共有A41A55=480种;
(2)∵甲、乙、丙不相邻,∴可以采用甲,乙和丙插空法,首先排列除去甲,乙和丙之外的三个人,有A33种结果,再在三个元素形成的四个空中排列3个元素,共有A43,根据分步计数原理知共有A33A43=144种.
(1)甲不站排头也不站排尾,甲要站在除去排头和排尾的四个位置,余下的五个位置使五个元素全排列,根据分步计数原理得到结果.
(2)甲、乙、丙不相邻,可以采用甲,乙和丙插空法,首先排列除去甲,乙和丙之外的三个人,有A33种结果,再在三个元素形成的四个空中排列3个元素,共有A43,根据分步计数原理得到结果.
解:
(1)∵甲不站排头也不站排尾,∴甲要站在除去排头和排尾的四个位置,余下的五个位置使五个元素全排列,根据分步计数原理知共有A41A55=480种;
(2)∵甲、乙、丙不相邻,∴可以采用甲,乙和丙插空法,首先排列除去甲,乙和丙之外的三个人,有A33种结果,再在三个元素形成的四个空中排列3个元素,共有A43,根据分步计数原理知共有A33A43=144种.

练习册系列答案
相关题目
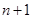 个球(其中
个球(其中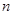 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出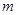 个球
个球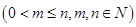 ,共有
,共有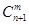 种取法,这
种取法,这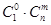 种取法,另一类是取出的
种取法,另一类是取出的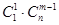 种取法,由此可得等式:
种取法,由此可得等式: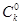 ·
·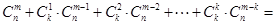 .
. 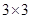 方格中的9个区域,要求每行每列的三个区域都不同色,则不同的填涂种数共有
方格中的9个区域,要求每行每列的三个区域都不同色,则不同的填涂种数共有 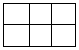
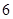
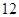
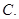
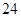
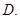
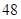
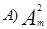 ;
; 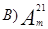 ;
; 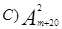 ;
;