题目内容
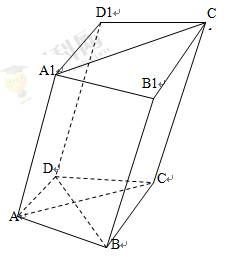
如图,在四棱柱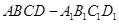 中,已知平面
中,已知平面 ,且
,且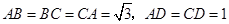 .
.
(1)求证: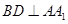 ;
;
(2)在棱BC上取一点E,使得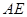 ∥平面
∥平面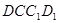 ,求
,求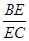 的值.
的值.
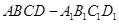 中,已知平面
中,已知平面 ,且
,且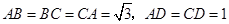 .
.
(1)求证:
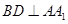 ;
;(2)在棱BC上取一点E,使得
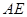 ∥平面
∥平面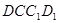 ,求
,求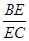 的值.
的值.(1)证明参考解析;(2)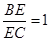
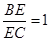
试题分析:(1)由于AB=CB,AD=CD,BD=BD.可得三角形ABD全等于三角形CBD.所以这两个三角形关于直线BD对称.所以可得
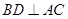 .再由面面垂直即可得直线BD垂直于平面
.再由面面垂直即可得直线BD垂直于平面 .从而可得
.从而可得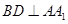 .
.(2)由于AC=
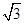 .AD=CD=1.所以可得角ACD等于300.又因为角ACB等于600.所以可得角DCB为直角.所以取BC边上的中点即为所求的点.本题考查的知识点是面面垂直线面垂直即线面平行.以及一个开放性的问题.
.AD=CD=1.所以可得角ACD等于300.又因为角ACB等于600.所以可得角DCB为直角.所以取BC边上的中点即为所求的点.本题考查的知识点是面面垂直线面垂直即线面平行.以及一个开放性的问题.试题解析:证明:(1)在四边形ABCD中,因为BA=BC,DA=DC,所以
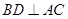 .
.平面
 ,且
,且
所以
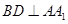 .
.(2)点E为BC中点,即
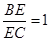 ,
,下面给予证明:在三角形ABC中,因为AB=AC,却E为BC中点,所以
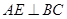 ,
,又在四边形ABCD中,AB=BC=CA=
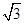 ,DA=DC=1,所以
,DA=DC=1,所以 ,
,所以
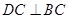 ,即平面ABCD中有,
,即平面ABCD中有, .
.因为
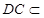 平面
平面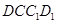 .AE
.AE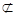 平面
平面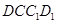 .
.所以 AE∥平面
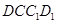 .
.
练习册系列答案
相关题目
 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE=x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .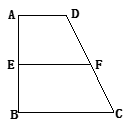
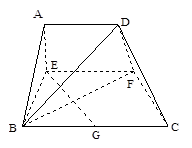
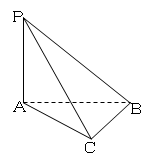
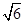 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为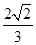 ,PB与底面ABC成60°角,求二面角B―PC―A的大小。
,PB与底面ABC成60°角,求二面角B―PC―A的大小。 中,
中,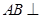 平面
平面 ,
,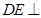 平面
平面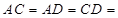
 ,
,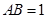 ,
, 为
为 的中点.
的中点.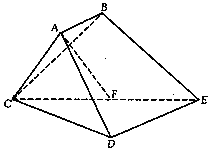
 ;
; 与平面
与平面 所成角的余弦值的大小.
所成角的余弦值的大小.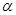 和
和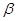 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: 与
与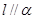 ;
;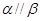 ;
;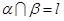 ,若
,若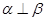 ;
;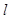 与平面
与平面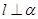 .
.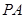 垂直于⊙
垂直于⊙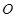 所在的平面,
所在的平面,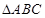 内接于⊙
内接于⊙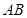 为⊙
为⊙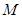 为线段
为线段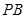 的中点.现有结论:①
的中点.现有结论:①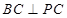 ;②
;② 平面
平面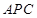 ;③点
;③点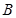 到平面
到平面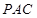 的距离等于线段
的距离等于线段 的长.其中正确的是( )
的长.其中正确的是( )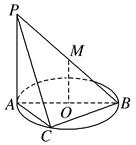
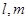 ,平面
,平面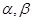 ,且
,且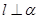 ,
,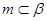 ,给出下列四个命题:
,给出下列四个命题: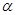 ∥
∥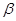 ,则
,则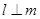 ;
;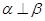 ,则
,则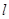 ∥
∥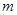 ;
;