题目内容
已知向量 ,
, ,函数
,函数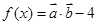 .
.
(1)若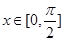 ,求
,求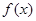 的最大值并求出相应
的最大值并求出相应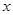 的值;
的值;
(2)若将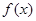 图象上的所有点的纵坐标缩小到原来的
图象上的所有点的纵坐标缩小到原来的 倍,横坐标伸长到原来的
倍,横坐标伸长到原来的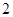 倍,再向左平移
倍,再向左平移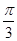 个单位得到
个单位得到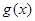 图象,求
图象,求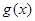 的最小正周期和对称中心;
的最小正周期和对称中心;
(3)若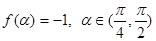 ,求
,求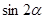 的值.
的值.
 ,
, ,函数
,函数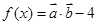 .
.(1)若
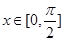 ,求
,求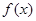 的最大值并求出相应
的最大值并求出相应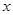 的值;
的值;(2)若将
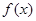 图象上的所有点的纵坐标缩小到原来的
图象上的所有点的纵坐标缩小到原来的 倍,横坐标伸长到原来的
倍,横坐标伸长到原来的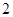 倍,再向左平移
倍,再向左平移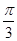 个单位得到
个单位得到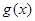 图象,求
图象,求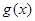 的最小正周期和对称中心;
的最小正周期和对称中心;(3)若
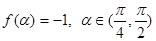 ,求
,求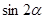 的值.
的值.(1) 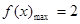 ,
,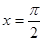 ;(2)
;(2)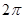 ,
,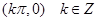 (3)
(3) 。
。
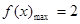 ,
,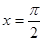 ;(2)
;(2)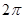 ,
,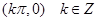 (3)
(3) 。
。试题分析:根据向量数量积的坐标运算,可得
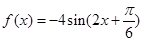 ,(1)由
,(1)由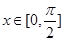 求出
求出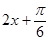 的
的范围,再利用正弦函数的单调性去求
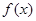 的最大值并求出相应
的最大值并求出相应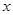 的值;(2)由伸缩变换、平移变换可得
的值;(2)由伸缩变换、平移变换可得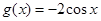 ;(3)
;(3)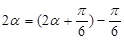 ,由
,由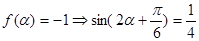 ,再利用
,再利用
求出
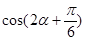 ,再利用两角差的正弦公式得
,再利用两角差的正弦公式得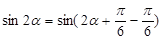
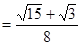 。
。试题解析:(1)
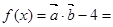
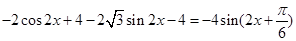 (2分)
(2分)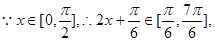 当
当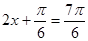 时,
时,即
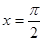 时
时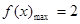 . (4分)
. (4分) (2)由题意
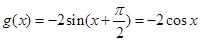 . (6分)
. (6分)∴
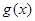 的最小正期为
的最小正期为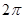 ,对称中心为
,对称中心为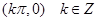 (8分)
(8分)(3)由
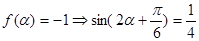 ,由
,由 得
得 ,
,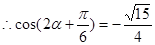 . (10分)
. (10分)所以
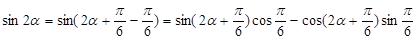
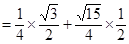
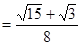 . (13分)
. (13分)
练习册系列答案
相关题目
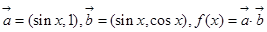
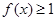 ,求x的范围;
,求x的范围;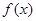 的最大值以及此时x的值.
的最大值以及此时x的值.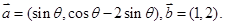
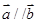 ,求
,求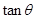 的值;
的值;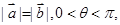 求
求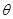 的值。
的值。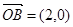 ,向量
,向量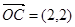 ,向量
,向量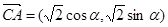 ,则向量
,则向量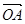 与向量
与向量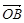 的夹角的取值范围是( )
的夹角的取值范围是( )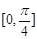
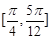
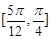
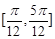
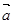
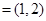 ,
,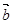
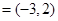 ,若向量
,若向量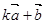 与
与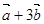 平行,则
平行,则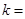 ______.
______.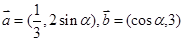 ,且
,且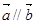 .若
.若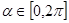 , 则
, 则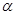 的值为
的值为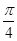
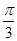
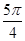
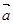 =(-3,2),
=(-3,2),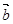 =(-1,0),向量
=(-1,0),向量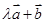 与
与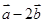 垂直,则实数
垂直,则实数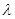 的值为 .
的值为 .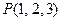 关于坐标平面
关于坐标平面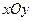 对称点
对称点 的坐标为
的坐标为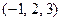
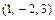
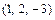
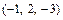
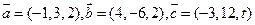 ,若
,若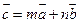 ,
,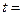 .
.