题目内容
(1)已知cos(2α+β)+5cosβ=0,求tan(α+β)·tanα的值;
(2)已知 ,求
,求 的值。
的值。
(2)已知
 ,求
,求 的值。
的值。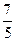
:从变换角的差异着手。∵ 2α+β=(α+β)+α,β=(α+β)-α
∴ 8cos[(α+β)+α]+5cos[(α+β)-α]=0
展开得:13cos(α+β)cosα-3sin(α+β)sinα=0
同除以cos(α+β)cosα得:tan(α+β)tanα=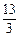
(1)以三角函数结构特点出发∵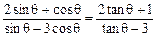 ∴
∴ 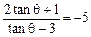
∴ tanθ=2∴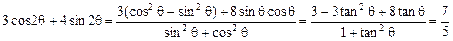
注;齐次式是三角函数式中的基本式,其处理方法是化切或降幂。
∴ 8cos[(α+β)+α]+5cos[(α+β)-α]=0
展开得:13cos(α+β)cosα-3sin(α+β)sinα=0
同除以cos(α+β)cosα得:tan(α+β)tanα=
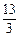
(1)以三角函数结构特点出发∵
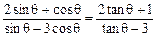 ∴
∴ 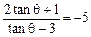
∴ tanθ=2∴
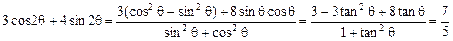
注;齐次式是三角函数式中的基本式,其处理方法是化切或降幂。

练习册系列答案
相关题目
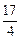 ,求a的取值范围。
,求a的取值范围。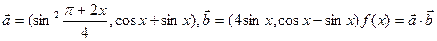
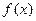 的解析式
的解析式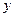 轴的正半轴及
轴的正半轴及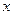 轴的正半轴三者围成图形的面积
轴的正半轴三者围成图形的面积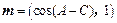 和
和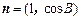 满足
满足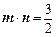 .
.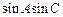 的值;
的值; 点发现乙船在北偏东60度的
点发现乙船在北偏东60度的 点处,测得乙船以每小时
点处,测得乙船以每小时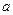 海里的速度向正北行驶,
海里的速度向正北行驶, 海里,则甲船如何航行才能最快地与乙船相遇?
海里,则甲船如何航行才能最快地与乙船相遇?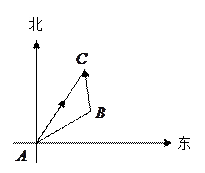

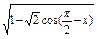 的定义域和值域.
的定义域和值域.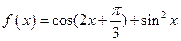 。
。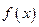 的最小正周期,并判断奇偶性;
的最小正周期,并判断奇偶性;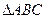 的三个内角,若
的三个内角,若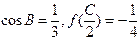 ,且C为锐角,求
,且C为锐角,求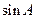 。
。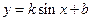 的最大值为
的最大值为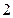 ,最小值为
,最小值为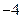 ,求
,求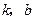 的值.
的值.