题目内容
（本小题满分12分）
已知数列{
} 的前n项和
，数列{
}的前n项和
（Ⅰ）求数列{}与{}的通项公式；
（Ⅱ）设
，证明：当且仅当n≥3时，
＜
w.w.w.k.s.5.u.c.o.m 
【思路】由
可求出
，这是数列中求通项的常用方法之一，在求出后，进而得到
，接下来用作差法来比较大小，这也是一常用方法。
解析：(1)由于
当
时, 
又当
时
数列
项与等比数列,其首项为1,公比为
w.w.w.k.s.5.u.c.o.m 
(2)由(1)知
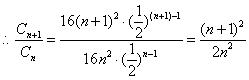
由
即
即
又时
成立,即
由于
恒成立. w.w.w.k.s.5.u.c.o.m
因此,当且仅当时, 
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
