题目内容
(本题10分)
已知函数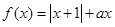 (
(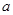 ∈R).
∈R).
(1)试给出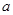 的一个值,并画出此时函数的图象;
的一个值,并画出此时函数的图象;
(2)若函数 f (x) 在 R 上具有单调性,求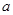 的取值范围.
的取值范围.
【答案】
(1)略
(2)a的取值范围是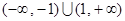 .
.
【解析】(1)解:略
(2)解:
化简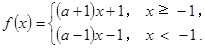
① a >1时,
当x ≥-1 时,
时,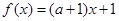 是增函数,且
是增函数,且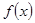 ≥
≥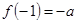 ;
;
当x < -1时,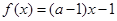 是增函数,且
是增函数,且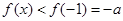 .
.
所以,当a >
 1时,函数f (x) 在R上是增函数.
1时,函数f (x) 在R上是增函数.
同理可知,当a <-1时,函数f (x) 在R上是减函数.
② a =1或-1时,易知,不合题意.
a =1或-1时,易知,不合题意.
③  -1< a <1时,取x = 0,得f (0) =1,取x =
-1< a <1时,取x = 0,得f (0) =1,取x =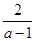 ,由
,由
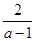 < -1,知f (
< -1,知f (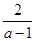 )
=1,
)
=1,
所以f (0) = f (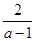 ).
).
所以函数f (x) 在R上不具有单调性.
综上可知,a的取值范围是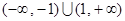 .
.

练习册系列答案
相关题目
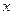 的不等式
的不等式 (Ⅰ)当
(Ⅰ)当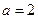 时,解不等式;
时,解不等式;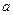 的取值范围。
的取值范围。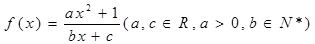 是奇
是奇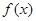 有最小值2,且f (1)
有最小值2,且f (1) .
.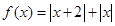
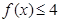 ;
;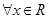 ,恒有
,恒有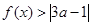 成立,求
成立,求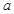 的取值范围.
的取值范围.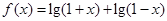
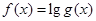 ,判断函数
,判断函数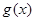 在
在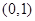 上的单调性并用定义证明
上的单调性并用定义证明