题目内容
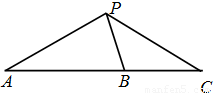
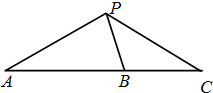 如图,B是△PAC的边AC上一点,且AB=2BC=4,∠APB=90°,∠CPB=30°,则
如图,B是△PAC的边AC上一点,且AB=2BC=4,∠APB=90°,∠CPB=30°,则| PA |
| PC |
-6
-6
.分析:设PB长为x,在△PBC中利用正弦定理,算出
=
x.再在△PBC中算出sinC关于x的式子,利用正弦定理建立关于x的方程,解出x的值,从而得到向量
、
的长度,结合数量积的计算公式,得到所求的结果.
| |PC| |
| 3 |
| PA |
| PC |
解答:解:设
=x,
则Rt△PAB中,
=
,sinA=
=
∵△PBC中,
=
∴
=
x
sin∠PBC=sin∠PBA=cosA=
,cos∠PBC=-cos∠PBA=-sinA=-
∴sinC=sin(∠PBC+∠BPC)=
cos30°+(-
)sin30°=
在△PBC中,
=
,即
=
解之得:x=2,所以
=
=2
,
=
x=2
∴
•
=
•
cos120°=2
•2
•(-
)=-6
故答案为:-6
| |PB| |
则Rt△PAB中,
| |PA| |
| 16-x2 |
| ||
|
| x |
| 4 |
∵△PBC中,
| AC |
| sin120° |
| PC |
| sinA |
∴
| |PC| |
| 3 |
sin∠PBC=sin∠PBA=cosA=
| ||
| 4 |
| x |
| 4 |
∴sinC=sin(∠PBC+∠BPC)=
| ||
| 4 |
| x |
| 4 |
| ||
| 8 |
在△PBC中,
| PB |
| sinC |
| BC |
| sin∠CPB |
| x | ||||
|
| 2 |
| sin30° |
解之得:x=2,所以
| |PA| |
| 16-22 |
| 3 |
| |PC| |
| 3 |
| 3 |
∴
| PA |
| PC |
| |PA| |
| |PC| |
| 3 |
| 3 |
| 1 |
| 2 |
故答案为:-6
点评:本题在特殊三角形中求向量的数量积,着重考查了正弦定理解三角形和向量数量积的运算等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
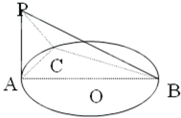 如图:AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,
如图:AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,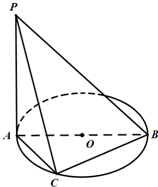 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点. (2)若
(2)若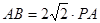 ,∠ABC=30°,求二面角A—PB—C的大小.
,∠ABC=30°,求二面角A—PB—C的大小.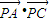 = .
= .