Question

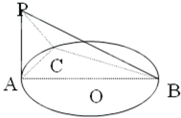如图：AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的任意一点，
（1）求证：平面PAC⊥平面PBC．
（2）图中有几个直角三角形．

Answer 1

分析：（1）利用直径所对的圆周角的性质、线面与面面垂直的判定和性质定理即可证明；
（2）利用（1）的结论和线面垂直的性质定理即可判断出答案．

解答：解：（1）∵PA⊥平面ABC，∴PA⊥BC，
又∵∠ACB是直径AB所对的圆周角，∴∠ACB=90°，∴BC⊥AC．
∵AP∩AC=A，∴BC⊥平面PAC．
∵BC?平面PBC，∴平面PAC⊥平面PBC．
（2）图中有4个直角三角形．证明如下：
①由（1）可知：BC⊥平面PAC，∴BC⊥PC，∴△PBC是直角三角形；
②∵PA⊥平面ABC，∴PA⊥AB，PA⊥AC，∴△PAB和△PAC都是直角三角形；
③由（1）可知：∠ACB=90°，∴△ACB是直角三角形．
综上可知：此三棱锥P-ABC的四个面都是直角三角形．

点评：熟练掌握直径所对的圆周角的性质、线面与面面垂直的判定和性质定理是解题的关键．