题目内容
 如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为
如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为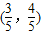 ,点B在第二象限,且△AOB为正三角形.
,点B在第二象限,且△AOB为正三角形.(Ⅰ)求sin∠COA;
(Ⅱ)求△BOC的面积.
【答案】分析:(I)由三角函数在单位圆中的定义可以知道,当一个角的终边与单位圆的交点坐标时,这个点的纵标就是角的正弦值.
(II)根据第一问所求的角的正弦值和三角形是一个等边三角形,利用两个角的和的正弦公式摸到的这个角的正弦值,根据正弦定理做出三角形的面积.
解答:解:(I)由三角函数在单位圆中的定义可以知道,
当一个角的终边与单位圆的交点是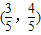 ,
,
∴sin∠COA= ,
,
(II)∵∠BOC=∠BOA+∠AOC,
∴sin∠BOC=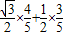 =
=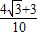
∴三角形的面积是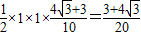
点评:本题考查单位圆和三角函数的定义,是一个基础题,这种题目解题的关键是正确使用单位圆,注意数字的运算不要出错.
(II)根据第一问所求的角的正弦值和三角形是一个等边三角形,利用两个角的和的正弦公式摸到的这个角的正弦值,根据正弦定理做出三角形的面积.
解答:解:(I)由三角函数在单位圆中的定义可以知道,
当一个角的终边与单位圆的交点是
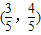 ,
,∴sin∠COA=
 ,
,(II)∵∠BOC=∠BOA+∠AOC,
∴sin∠BOC=
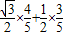 =
=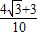
∴三角形的面积是
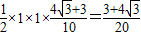
点评:本题考查单位圆和三角函数的定义,是一个基础题,这种题目解题的关键是正确使用单位圆,注意数字的运算不要出错.

练习册系列答案
相关题目
 已知偶函数f(x)在(0,+∞)上的图象如图,则下列函数中与f(x)在(-∞,0)上单调性不同的是( )
已知偶函数f(x)在(0,+∞)上的图象如图,则下列函数中与f(x)在(-∞,0)上单调性不同的是( )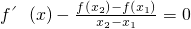 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解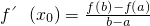 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明: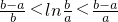 (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).


 在(x1,x2)恒有实数解
在(x1,x2)恒有实数解 .如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
.如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明: (可不用证明函数的连续性和可导性).
(可不用证明函数的连续性和可导性).