题目内容
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
B
解析试题分析: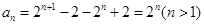 .
.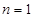 时,
时,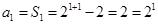 ,故
,故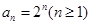 .所以
.所以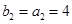 ,由此可排除A、C、D.
,由此可排除A、C、D.
对B选项,若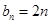 ,则
,则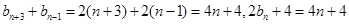 满足题设,选B.
满足题设,选B.
考点:数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
观察下列数的特点,1,1,2,3,5,8,x,21,34,55,…中,其中x是( )
| A.12 | B.13 | C.14 | D.15 |
已知数列 对任意的
对任意的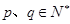 满足
满足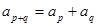 且
且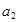 =6,那么
=6,那么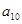 等于( )
等于( )
| A.165 | B.33 | C.30 | D.21 |
数列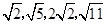 的一个通项公式是( )
的一个通项公式是( )
A.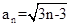 | B.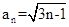 | C.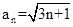 | D.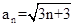 |
设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,…
若b1>c1,b1+c1=2a1,an+1=an,bn+1=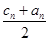 ,cn+1=
,cn+1= ,则( )
,则( )
| A.{Sn}为递减数列 |
| B.{Sn}为递增数列 |
| C.{S2n-1}为递增数列,{S2n}为递减数列 |
| D.{S2n-1}为递减数列,{S2n}为递增数列 |
设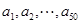 是从-1,0,1这三个整数中取值的数列,若
是从-1,0,1这三个整数中取值的数列,若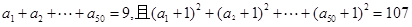 ,则
,则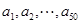 中数字0的个数为( )
中数字0的个数为( )
| A.11 | B.12 | C.13 | D.14 |
 ,
,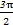 ).
). |=|
|=|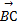 |,求角α的值.
|,求角α的值.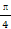 )的值.
)的值.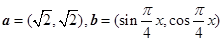
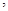 若函数
若函数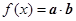 .
. 的最小正周期;
的最小正周期;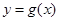 的图象,若函数
的图象,若函数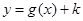 在
在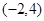 上有两个零点,求实数
上有两个零点,求实数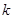 的取值范围.
的取值范围. 中,对任意正整数
中,对任意正整数 ,都有
,都有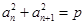 (常数),则称数列
(常数),则称数列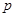 为“公方和”,若数列
为“公方和”,若数列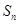 ,且“公方和”为
,且“公方和”为 ,首项
,首项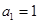 ,则
,则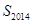 的最大值与最小值之和为( )
的最大值与最小值之和为( )