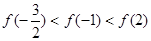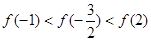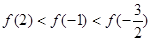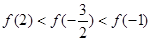题目内容
设定义域为R的函数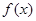 满足下列条件:对任意
满足下列条件:对任意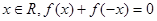 ,且对任意
,且对任意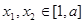
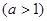 ,当
,当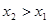 时,有
时,有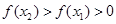 .给出下列四个结论:
.给出下列四个结论:
①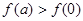 ②
②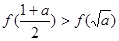
③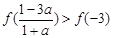 ④
④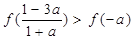
其中所有的正确结论的序号是____________.
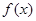 满足下列条件:对任意
满足下列条件:对任意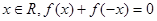 ,且对任意
,且对任意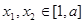
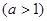 ,当
,当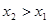 时,有
时,有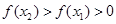 .给出下列四个结论:
.给出下列四个结论:①
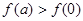 ②
②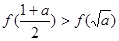
③
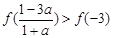 ④
④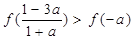
其中所有的正确结论的序号是____________.
①②④
试题分析:∵对任意x∈R,f(x)+f(-x)=0,∴函数f(x)是奇函数,∵对任意x1,x2∈[1,a],当x2>x1时,有f(x2)>f(x1)>0,∴函数f(x)在区间[1,a]上是单调增函数.∵a>1,故①f(a)>f(0)一定成立.
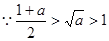 ,故②
,故②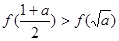 一定成立.
一定成立.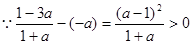 ,
,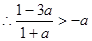 ,
,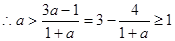
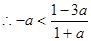 ,由奇函数的对称性知:
,由奇函数的对称性知: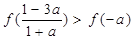 ,④对.
,④对.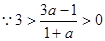 ,但
,但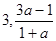 是否在[1,a]上不能确定,故意
是否在[1,a]上不能确定,故意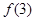 和
和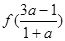 的大小不能确定,③不对,故正确的为①②④.
的大小不能确定,③不对,故正确的为①②④.
练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
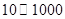 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金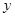 (单位:万元)随投资收益
(单位:万元)随投资收益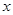 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于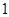 万元,同时不超过投资收益的
万元,同时不超过投资收益的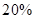 .
.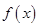 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型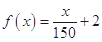 ; ②
; ②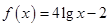
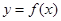 在[0,+∞)上是减函数,试比较
在[0,+∞)上是减函数,试比较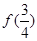 与
与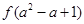 的大小.
的大小.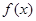 是定义在R上的奇函数且单调递减,若
是定义在R上的奇函数且单调递减,若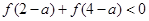 ,则
,则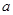 的取值范围是( )
的取值范围是( )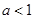
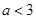
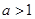
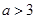
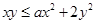 对于
对于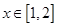 ,
,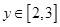 恒成立,则实数
恒成立,则实数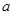 的取值范围是___________.
的取值范围是___________.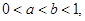 则下列不等式成立的是( )
则下列不等式成立的是( )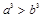
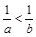

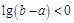
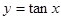
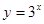
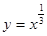
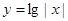
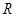 上的函数
上的函数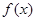 是最小正周期为
是最小正周期为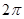 的偶函数,
的偶函数,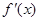 是
是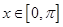 时,
时,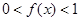 ;当
;当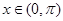 且
且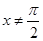 时 ,
时 ,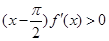 ,则函数
,则函数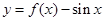 在
在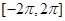 上的零点个数为( )
上的零点个数为( )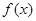 在
在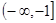 上是增函数,则下列关系式中成立的是( )
上是增函数,则下列关系式中成立的是( )