题目内容
若函数 满足
满足 ,且x∈[-1,1]时,
,且x∈[-1,1]时,
f(x) =l—x2,函数 则函数h(x)=f(x)一g(x)在区间[-5,5]内的与x轴交点的个数为
则函数h(x)=f(x)一g(x)在区间[-5,5]内的与x轴交点的个数为
| A.5 | B.7 | C.8 | D.10 |
C
解析试题分析: 因为函数 满足
满足 ,因此其周期为2,且x∈[-1,1]时,
,因此其周期为2,且x∈[-1,1]时,
f(x) =l—x2,函数
而函数h(x)=f(x)一g(x)在区间[-5,5]内的与x轴交点的个数可以转化为求解函数y=f(x)与y=g(x的交点问题来处理,那么作图可知,符合题意的交点个数有8个。选C.
考点:本题主要考查了函数与方程的思想的运用。
点评:解决该试题的关键是对于函数与方程的根的问题,转化为函数图像与函数图像的交点的问题的运用,同时对数抽象函数的周期性的准确理解和运用。

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
若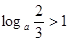 ,则a的取值范围是( )
,则a的取值范围是( )
A.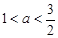 | B.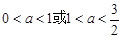 |
C.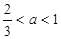 | D.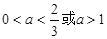 |
函数y= 的值域是[-2,2],则函数y=
的值域是[-2,2],则函数y=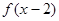 的值域是( )
的值域是( )
| A.[-2,2] | B.[-4,0] | C.[0,4] | D.[-1,1] |
设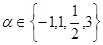 ,则使函数
,则使函数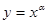 的定义域为
的定义域为 且为奇函数的所有
且为奇函数的所有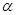 的值为( )
的值为( )
| A.1,3 | B.-1,1 | C.-1,3 | D.-1,1,3 |
函数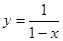 的图像与函数
的图像与函数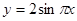 (
(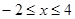 )的图像所有交点的横坐标之和等于 ( )
)的图像所有交点的横坐标之和等于 ( )
| A.2 | B.4 | C.6 | D.8 |
设 的零点为
的零点为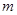 ,则
,则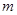 所在的区间为( )
所在的区间为( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
函数 的定义域为
的定义域为
A. | B. | C. | D. |
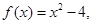
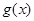 是定义在
是定义在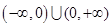 上的奇函数,当
上的奇函数,当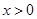 时,
时,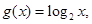 则函数
则函数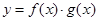 的大致图象为
的大致图象为
 的图象只可能是 ( )
的图象只可能是 ( )