题目内容
已知函数f(x)=x2-2x,则满足条件 的点(x,y)所形成区域的面积为( )
的点(x,y)所形成区域的面积为( )A.4π
B.2π
C.

D.π
【答案】分析:我们由f(x)=x2-2x,我们可以先画出满足约束条件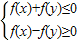 的可行域,然后分析可行域的形状,然后代入面积公式求出可行域的面积.
的可行域,然后分析可行域的形状,然后代入面积公式求出可行域的面积.
解答: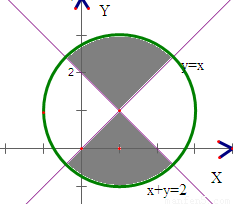 解:∵f(x)=x2-2x
解:∵f(x)=x2-2x
∴约束条件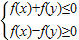
可以转化为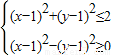 ,
,
其对应的可行域如下图示:
其面积为: •π•
•π•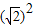 =π
=π
故选D.
点评:平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.
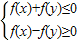 的可行域,然后分析可行域的形状,然后代入面积公式求出可行域的面积.
的可行域,然后分析可行域的形状,然后代入面积公式求出可行域的面积.解答:
 解:∵f(x)=x2-2x
解:∵f(x)=x2-2x∴约束条件
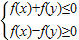
可以转化为
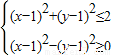 ,
,其对应的可行域如下图示:
其面积为:
 •π•
•π•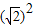 =π
=π故选D.
点评:平面区域的面积问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后结合有关面积公式求解.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|