题目内容
【题目】已知函数![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() ,求实数a的取值范围;
,求实数a的取值范围;
![]() 当
当![]() 时,曲线
时,曲线![]() 和曲线
和曲线![]() 是否存在公共切线?并说明理由.
是否存在公共切线?并说明理由.
【答案】(1)![]() ;(2)存在公共切线,理由详见解析.
;(2)存在公共切线,理由详见解析.
【解析】
(1)构造函数![]() ,求出其最大值,解不等式即可得到实数
,求出其最大值,解不等式即可得到实数![]() 的取值范围;
的取值范围;
(2)假设存在这样的直线![]() 且直线
且直线![]() 与曲线和曲线
与曲线和曲线![]() 分别相切与点
分别相切与点![]() .分别求出两条切线方程,根据斜率与纵截距建立方程组,减元后得到
.分别求出两条切线方程,根据斜率与纵截距建立方程组,减元后得到![]() ,构造新函数研究单调性与极值即可.
,构造新函数研究单调性与极值即可.
解:![]() 令
令![]() ,则
,则![]() .
.
若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
所以![]() 是
是![]() 的极大值点,也是
的极大值点,也是![]() 的最大值点,即
的最大值点,即![]() .
.
若![]() 恒成立,则只需
恒成立,则只需![]() ,解得
,解得![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.
![]() 假设存在这样的直线
假设存在这样的直线![]() 且与曲线
且与曲线![]() 和曲线
和曲线![]() 分别相切与点
分别相切与点![]() .
.
由![]() ,得
,得![]() .
.
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
同理可得,
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
所以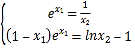 则
则![]() ,即
,即![]()
构造函数![]()
![]()
存在直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,
相切,
等价于函数![]() 在
在![]() 上有零点
上有零点
对于![]() .
.
当![]() 时,
时,![]() ,
,![]() 在上单调递增.
在上单调递增.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 在
在![]() 上是减函数.
上是减函数.
又![]() ,,所以存在
,,所以存在![]() ,使得
,使得![]() ,即
,即![]() .
.
且当![]() ,
,![]() 时,当
时,当![]() 时,
时,![]() .
.
综上,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
所以![]() 是
是![]() 的极大值,也是最大值,且
的极大值,也是最大值,且![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 在
在![]() 内和
内和![]() 内各有一个零点.
内各有一个零点.
故假设成立,即曲线![]() 和曲线
和曲线![]() 存在公共切线.
存在公共切线.

练习册系列答案
相关题目
【题目】(2014·长春模拟)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差,并判断选谁参加比赛更合适?