题目内容
已知:函数f(x)=| ex |
| x-a |
(Ⅰ)求函数f(x)的定义域及单调区间;
(Ⅱ)若存在实数x∈(a,0],使得不等式f(x)≤
| 1 |
| 2 |
分析:(1)分式函数使分母不为零即{x|x≠a},先求导数fˊ(x),然后在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;确定出单调区间.
(2)转化成f(x)=
在(a,0]上的最小值小于等于
,利用导数求出函数f(x)=
在(a,0]上的最小值,注意讨论.
(2)转化成f(x)=
| ex |
| x-a |
| 1 |
| 2 |
| ex |
| x-a |
解答:解:(Ⅰ)函数f(x)的定义域为{x|x≠a}.(1分)
f′(x)=
=
.(3分)
由f'(x)>0,解得x>a+1.
由f'(x)<0,解得x<a+1且x≠a.
∴f(x)的单调递增区间为(a+1,+∞),
单调递减区间为(-∞,a),(a,a+1);(6分)
(Ⅱ)由题意可知,a<0,且f(x)=
在(a,0]上的最小值小于等于
时,
存在实数x∈(a,0],使得不等式f(x)≤
成立.(7分)
若a+1<0即a<-1时,
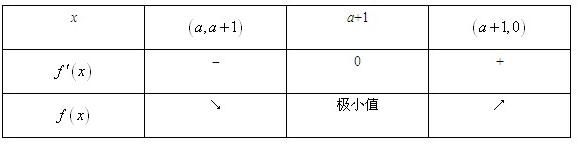
∴f(x)在(a,0]上的最小值为f(a+1)=ea+1.
则ea+1≤
,得a≤ln
-1.(10分)
若a+1≥0即a≥-1时,f(x)在(a,0]上单调递减,
则f(x)在(a,0]上的最小值为f(0)=-
.
由-
≤
得a≤-2(舍).(12分)
综上所述,a≤ln
-1.则a的取值范围是(-∞,ln
-1]
f′(x)=
| ex(x-a)-ex•1 |
| (x-a)2 |
| ex[x-(a+1)] |
| (x-a)2 |
由f'(x)>0,解得x>a+1.
由f'(x)<0,解得x<a+1且x≠a.
∴f(x)的单调递增区间为(a+1,+∞),
单调递减区间为(-∞,a),(a,a+1);(6分)
(Ⅱ)由题意可知,a<0,且f(x)=
| ex |
| x-a |
| 1 |
| 2 |
存在实数x∈(a,0],使得不等式f(x)≤
| 1 |
| 2 |
若a+1<0即a<-1时,

∴f(x)在(a,0]上的最小值为f(a+1)=ea+1.
则ea+1≤
| 1 |
| 2 |
| 1 |
| 2 |
若a+1≥0即a≥-1时,f(x)在(a,0]上单调递减,
则f(x)在(a,0]上的最小值为f(0)=-
| 1 |
| a |
由-
| 1 |
| a |
| 1 |
| 2 |
综上所述,a≤ln
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了函数的定义域、单调性以及利用导数求解恒成立问题,是高考中的热点问题.

练习册系列答案
相关题目
已知x0函数f(x)=(
)x-log2x的零点,若0<x1<x0,则f(x1)的值为( )
| 1 |
| 3 |
| A、恒为负值 | B、等于0 |
| C、恒为正值 | D、不大于0 |