Question

(本小题满分12分)

函数的定义域为[－1,2]，

（1）若，求函数的值域；（6分）

（2）若为非负常数，且函数是[－1,2]上的单调函数，求的范围及函数的值域。（6分）

 

Answer 1

【答案】

解：(1) 当a=2时，f(x)=-2x2+4x+1=-2(x-1)2+3           …2分

当x∈[-1,1]时，f(x)单调递减，当x∈[-1,2]时，f(x)单调递增，

f(x)max=f(1)= 3,又∵ f(-1)=-5,f(2)=1,∴f(x)min=f(-1)=-5,

∴f(x)的值域为[-5,3]                                              ……6分

  (2) 当a=0时，f(x)=4x+1,在[-1，2]内单调递增,∴值域为[-3, 9]。    ……7分

当a>0时，f(x)= 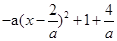,                           ……8分

又f(x) 在[-1,2]内单调 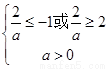 ∴  解得0<a≤1    

综上：0≤a≤1                                                 ……10分

   当0≤a≤1， f(x)在[-1，2]内单调递增，∴值域为[-a-3,-4a+9]

f(x)min=f(-1)=-a-3,f(x)max=f(2)= -4a+9, ∴值域为[-a-3,-4a+9]

 ∴a的取值范围是[0,1]，f(x)值域为 [-a-3,-4a+9]                  -----12分

 

【解析】略