题目内容
【题目】长方体![]() 中,
中,![]()
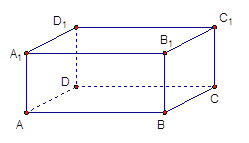
(1)求直线![]() 与
与![]() 所成角;
所成角;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦.
所成角的正弦.
【答案】(1)直线![]() 所成角为90°;(2)
所成角为90°;(2)![]() 。
。
【解析】
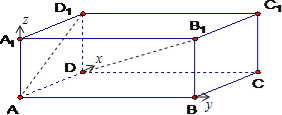
试题(1)建立空间直角坐标系,求出直线AD1与B1D的方向向量,利用向量的夹角公式,即可求直线AD1与B1D所成角;
(2)求出平面B1BDD1的法向量,利用向量的夹角公式,即可求直线AD1与平面B1BDD1所成角的正弦.
解:(1)建立如图所示的直角坐标系,则A(0,0,0),D1(1,0,1),B1(0,2,1),D(1,0,0).
∴![]() ,
,
∴cos![]() =
=![]() =0,
=0,
∴![]() =90°,
=90°,![]()
∴直线AD1与B1D所成角为90°;
(2)设平面B1BDD1的法向量![]() =(x,y,z),则
=(x,y,z),则
∵![]() ,
,![]() =(﹣1,2,0),
=(﹣1,2,0),
∴![]() ,
,
∴可取![]() =(2,1,0),
=(2,1,0),
∴直线AD1与平面B1BDD1所成角的正弦为![]() =
=![]() .
.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目