题目内容
若θ是第二象限的角,且cos
<0,那么
的值是( )
| θ |
| 2 |
| ||||
sin
|
| A、-1 | ||
B、
| ||
| C、1 | ||
| D、2 |
分析:化简
,然后根据θ是第二象限的角,且cos
<0,确定
的范围,确定sin
-cos
的符号,可得结果.
| ||||
sin
|
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
解答:解:
=
θ是第二象限的角,且cos
<0,
所以kπ+
<
<kπ+
k∈Z是第三象限的角,
sin
-cos
<0
=-1
故选A.
| ||||
sin
|
| ||||||
sin
|
θ是第二象限的角,且cos
| θ |
| 2 |
所以kπ+
| 3π |
| 4 |
| θ |
| 2 |
| 3π |
| 2 |
sin
| θ |
| 2 |
| θ |
| 2 |
| ||||
sin
|
故选A.
点评:本题考查同角三角函数的基本关系式,象限角,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 ,
, .
. 的最大值和最小正周期;
的最大值和最小正周期; ,
, 是第二象限的角,求
是第二象限的角,求 .
. 的最小正周期是
的最小正周期是 ,其中ω>0.
,其中ω>0. ,α是第二象限的角,求sin2α.
,α是第二象限的角,求sin2α. 的最小正周期是
的最小正周期是 ,其中ω>0.
,其中ω>0. ,α是第二象限的角,求sin2α.
,α是第二象限的角,求sin2α. .(1)求
.(1)求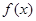 的最大值和最小正周期;(2) 若
的最大值和最小正周期;(2) 若 ,
, 是第二象限的角,求
是第二象限的角,求 .
.