题目内容
4. 如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,底面边长和侧棱长均为2,D,D1分别是BC,B1C1的中点.
如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,底面边长和侧棱长均为2,D,D1分别是BC,B1C1的中点.(1)求证:AD⊥C1D;
(2)求证:平面ADC1∥平面A1D1B.
分析 (1)线面垂直的判定定理证明即可;
(2)根据面面平行的判定定理证明即可.
解答  (1)证明:∵底面边长均为2,D是BC中点,∴AD⊥BC-----------------(1分)
(1)证明:∵底面边长均为2,D是BC中点,∴AD⊥BC-----------------(1分)
∵三棱柱ABC-A1B1C1的侧棱垂直于底面,AD?平面ABC,
∴AD⊥BB1---------------(2分)
∵BC?平面B1BCC1,BB1?平面B1BCC1,BC∩BB1=B,
∴AD⊥平面B1BCC1,--------------(3分)
∵DC1?面B1BCC1,
∴AD⊥DC1-----------(4分)
(2)证明:连结A1C交于AC1O,连结DO,如图示:
∵O是正方形ACC1A1对角线的交点
∴O为A1C中点
∵D是BC的中点
∴OD∥A1B,且OD?平面ADC1,A1B?平面ADC1--------------(6分)
∴A1B∥平面ADC1-------------------(7分)
∵D,D1分别是BC,B1C1的中点,
∴AA1∥DD1,AA1=DD1,
∴四边形AA1D1D是平行四边形
∴AD∥A1D1-----(9分)
∵A1D1?平面ADB1,AD?平面ADB1,
∴A1D1∥平面ADB1---------(10分)
∵A1D1∩A1B=A1,
∴平面ADC1∥平面A1D1B-----------------(12分)
点评 本题考查了线面垂直的判定定理以及面面平行的判定定理,考查数形结合思想,是一道中档题.

练习册系列答案
相关题目
19.等式$\sqrt{\frac{x}{x-2}}=\frac{\sqrt{x}}{\sqrt{x-2}}$成立的条件是( )
| A. | x≠2 | B. | x>0 | C. | x>2 | D. | 0<x<2 |
14.函数y=$\frac{3sinx}{2cosx+1}$的定义域是( )
| A. | {x|x∈R} | B. | {x|x≠2kπ+$\frac{2π}{3}$} | ||
| C. | {x|x$≠2kπ+\frac{4π}{3},k∈Z$} | D. | {x|x≠2kπ+$\frac{2}{3}$π且x≠2kπ+$\frac{4}{3}π$,k∈Z] |
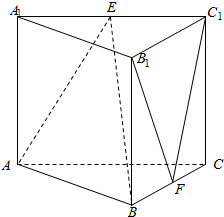 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F是A1C1、BC的中点.证明:
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F是A1C1、BC的中点.证明: