题目内容
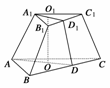
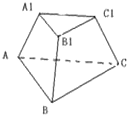
如图,正三棱台ABC-A1B1C1中,A1B1=2,AB=4.
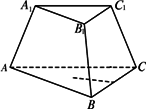
(1)若三棱台的高为3,A1B1=2,AB=4,求侧棱长及侧面与底面所成的角;
(2)若三棱台的高为h,A1B1∶AB=1∶2,过B1C1平行于相对侧棱AA1的截面把这个三棱台分成两部分,求这两部分的体积比.
答案:
解析:
解析:
|
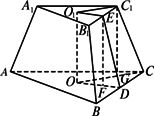
解:(1)如图,
设正三棱台ABC-A1B1C1上、下底面中心分别为点O1、O,作O1E⊥B1C1,垂足为E,ED⊥BC,垂足为D,EF⊥OD于点F,C1G⊥CO于点G. 在Rt△CC1G中,C1G=3, CG=CO-C1O1= ∴ 由作图可知,侧面与底面所成的角就是∠EDO. 在Rt△EDF中,EF=3, DF=DO-EO1= ∴tan∠EDF= ∴∠EDF=arctan (2)设截面B1C1NM∥A1A,则B1M∥A1A∥C1N,几何体A1B1C1-AMN为三棱柱.再设三棱台的上、下底面积分别为S1、S2.
∵△A1B1C1∽△ABC,且A1B1∶AB=1∶2, ∴S1∶S2=1∶4,即S2=4S1. ∴V三棱台= V三棱柱=S1h. ∴另一部分多面体的体积V=V三棱台-V三棱柱= ∴V三棱柱∶V=3∶4. |

练习册系列答案
相关题目
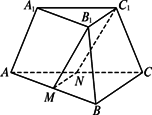
 如图所示,在正三棱台ABC-A1B1C1中,上、下底面的边长分别为3cm和6cm,高为
如图所示,在正三棱台ABC-A1B1C1中,上、下底面的边长分别为3cm和6cm,高为