题目内容
已知二次函数f(x)=ax2+bx满足f(x-1)=f(x)+x-1,
(1)求f(x)的解析式;
(2)求函数f(x)的零点,并写出f(x)<0时,x取值的集合;
(3)设F(x)=4f(ax)+3a2x-1(a>0,且a≠1),当x∈[-1,1]时,F(x)有最大值14,试求a的值.
(1)求f(x)的解析式;
(2)求函数f(x)的零点,并写出f(x)<0时,x取值的集合;
(3)设F(x)=4f(ax)+3a2x-1(a>0,且a≠1),当x∈[-1,1]时,F(x)有最大值14,试求a的值.
解:(1)∵f(x)=ax2+bx满足f(x-1)=f(x)+x-1,
∴a(x-1)2+b(x-1)=ax2+bx+x-1,
即ax2-(2a-b)x+a-b=ax2+(b+1)x-1,
∴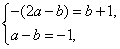 ,解得
,解得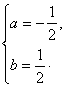 ,
,
∴ 。
。
(2)由f(x)=0得函数的零点为0,1,
又函数f(x)的图象是开口向下的抛物线,
∴f(x)<0时x>1或x<0,
∴x取值的集合为{x|x>1或x<0}.
(3)由F(x)=4f(ax)+3a2x-1(a>0,且a≠1),得F(x)=a2x+2ax-1,
①当a>1时,令u=ax,
∵x∈[-1,1],
∴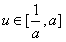 ,
,
令g(u)=u2+2u-1=(u+1)2-2,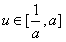 ,
,
∵对称轴u=-1,
∴g(u)在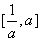 上是增函数,
上是增函数,
∴gmax(u)=g(a)=a2+2a-1=14,
∴a2+2a-15=0,
∴a=3,a=-5(舍);
②当0<a<1时,令u=ax,
∵x∈[-1,1],
∴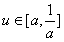 ,
,
∴g(u)=u2+2u-1=(u+1)2-2,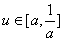 ,
,
∵对称轴u=-1,
∴g(u)在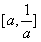 上是增函数,
上是增函数,
∴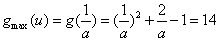 ,
,
∴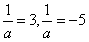 (舍),∴
(舍),∴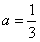 ;
;
综上,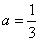 或a=3.
或a=3.
∴a(x-1)2+b(x-1)=ax2+bx+x-1,
即ax2-(2a-b)x+a-b=ax2+(b+1)x-1,
∴
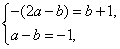 ,解得
,解得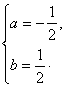 ,
,∴
 。
。(2)由f(x)=0得函数的零点为0,1,
又函数f(x)的图象是开口向下的抛物线,
∴f(x)<0时x>1或x<0,
∴x取值的集合为{x|x>1或x<0}.
(3)由F(x)=4f(ax)+3a2x-1(a>0,且a≠1),得F(x)=a2x+2ax-1,
①当a>1时,令u=ax,
∵x∈[-1,1],
∴
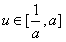 ,
,令g(u)=u2+2u-1=(u+1)2-2,
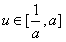 ,
,∵对称轴u=-1,
∴g(u)在
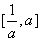 上是增函数,
上是增函数,∴gmax(u)=g(a)=a2+2a-1=14,
∴a2+2a-15=0,
∴a=3,a=-5(舍);
②当0<a<1时,令u=ax,
∵x∈[-1,1],
∴
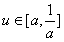 ,
,∴g(u)=u2+2u-1=(u+1)2-2,
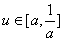 ,
,∵对称轴u=-1,
∴g(u)在
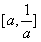 上是增函数,
上是增函数,∴
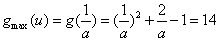 ,
,∴
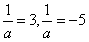 (舍),∴
(舍),∴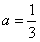 ;
;综上,
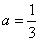 或a=3.
或a=3. 
练习册系列答案
相关题目