Question

【题目】已知抛物线经过点，过作直线与抛物线相切．

（1）求直线的方程；

（2）如图，直线∥，与抛物线交于，两点，与直线交于点，是否存在常数，使．

Answer 1

【答案】（1）（2）见解析

【解析】

（1）将T（2，2）代入y2＝2px，得抛物线方程，设直线l方程与抛物线方程联立，通过△＝0得k＝2，得直线l方程.（2）设直线l'的方程为y＝x+b，联立方程组解得P（2﹣2b，2﹣b），则PT2＝5b2，设A（x1，y1），B（x2，y2），与抛物线联立，利用弦长公式，转化求解即可．

（1）将代入，则，所以抛物线方程为．

设直线的方程为，联立方程组

消得，因相切，由得，

所以直线的方程为．

设直线的方程为，联立方程组

消得，因相切，由得，

所以直线的方程为．

（2）因，∥，设直线的方程为，联立方程组

解得，则．

设，，联立方程组得，

所以，；

，

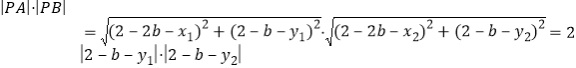
所以存在实数，使．