题目内容
10．已知函数f（x）=$\sqrt{9-6x+{x}^{2}}$+$\sqrt{{x}^{2}+8x+16}$（1）解不等式f（x）≥f（4）；
（2）设函数g（x）=kx-3k，k∈R，若不等式f（x）＞g（x）恒成立，求实数k的取值范围．
分析 （1）问题转化为解不等式|x-3|+|x+4|≥9，通过讨论x的范围，解出即可；（2）画出函数f（x），g（x）的图象，通过图象读出即可．
解答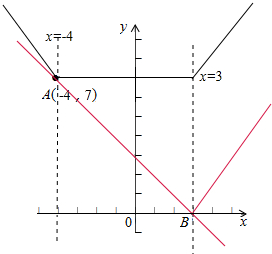 
解：（1）f（x）=$\sqrt{9-6x+{x}^{2}}$+$\sqrt{{x}^{2}+8x+16}$=|x-3|+|x+4|，f（4）=9，
∴问题转化为解不等式|x-3|+|x+4|≥9，
原不等式等价于
$\left\{\begin{array}{l}{x≤-4}\\{-2x-1≥9}\end{array}\right.$或$\left\{\begin{array}{l}{-4＜x＜3}\\{3-x+x+4≥9}\end{array}\right.$或$\left\{\begin{array}{l}{x≥3}\\{2x+1≥9}\end{array}\right.$，
解得，x≤-5或x≥4，
即不等式的解集为（-∞，-5]∪[4，+∞）．
（2）∵f（x）=$\left\{\begin{array}{l}{-2x-1，x≤-4}\\{7，-4＜x≤3}\\{2x+1，x＞3}\end{array}\right.$，g（x）=k（x-3），
画出函数f（x），g（x）的图象，如图示：
直线AB的斜率是；-1，
由其函数图象知：k∈（-1，2]．
点评 本题考查了绝对值不等式的解法，考查数形结合思想，是一道中档题．
练习册系列答案
相关题目
20．“x＞3”是“x＞2”的（ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
18．已知F1，F2是双曲线的两个焦点，P，Q是过点F1且垂直于实轴所在直线的双曲线的弦，∠PF2Q=90°，则双曲线的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{2}+1$ | C． | $\sqrt{2}-1$ | D． | $\frac{{\sqrt{2}}}{2}+1$ |