题目内容
(本小题满分12分)
在直三棱柱 中, AC=4,CB=2,AA1=2,
中, AC=4,CB=2,AA1=2,
 ,E、F分别是
,E、F分别是 的中点。
的中点。

(1)证明:平面 平面
平面 ;
;
(2)证明: 平面ABE;
平面ABE;
(3)设P是BE的中点,求三棱锥 的体积。
的体积。
【答案】
(1)对于面面垂直的证明,一般要通过线面垂直的证明来得到,分析条件得到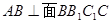 ,得到证明。
,得到证明。
(2)对于线面平行的证明,主要是利用线线平行来判定得到 。(3) 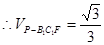
【解析】
试题分析:(1)证明:在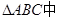 ,∵AC=2BC=4,
,∵AC=2BC=4,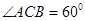 ∴
∴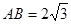
∴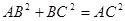 ∴
∴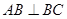 由已知
由已知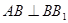
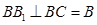
∴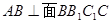
又∵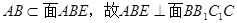
(2)证明:取AC的中点M,连结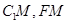 在
在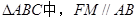 ,
,
∴ 直线FM//面ABE在矩形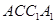 中,E、M都是中点 ∴
中,E、M都是中点 ∴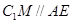
∴直线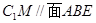 又∵
又∵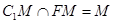 ∴
∴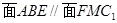
故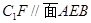
(3)在棱AC上取中点G,连结EG、BG,在BG上取中点O,
连结PO,则PO//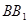 ,
, 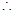 点P到面
点P到面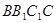 的距离等于点O到平面
的距离等于点O到平面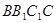 的距离。
的距离。
过O作OH//AB交BC与H,则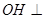 平面
平面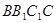 在等边
在等边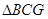 中可知
中可知
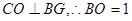 在
在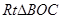 中,可得
中,可得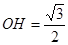
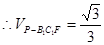
考点:立体几何中体积运算,以及面面位置关系的判定。
点评:解决该试题的关键是熟练的运用线面和面面的判定定理和性质定理解题,属于中档题。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目